Question

In the figure shown, $R=100\Omega$, $L=\dfrac{2}{\pi }H$ and $C=\dfrac{8}{\pi }\mu F$ are connected in series with an ac source of $200V$ and frequency $f$. ${{V}_{1}}$ and ${{V}_{2}}$ are two hot wire voltmeters. If the readings of ${{V}_{1}}$ and ${{V}_{2}}$ are same, then,

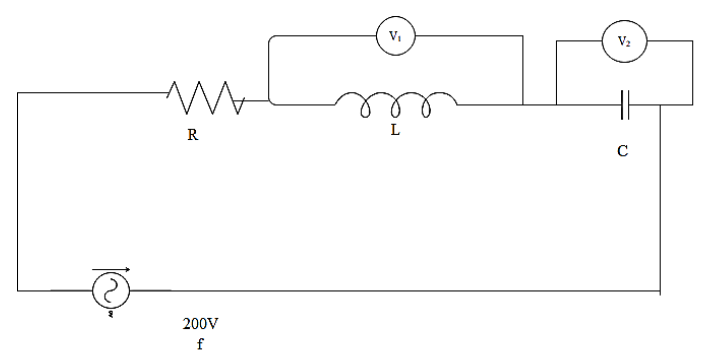
$\begin{aligned} & A.f=125Hz \\\ & B.f=250Hz \\\ & C.\text{current through R is }2A \\\ & D.{{V}_{1}}={{V}_{2}}=1000V \\\ \end{aligned}$

Answer 1

Hint The voltage across the inductor and capacitors are the same. Therefore the circuit will be in resonance. Frequency of the source can be found by taking the reciprocal of the product of the constant $2\pi$ and the square root of the product of the value of the inductance and capacitance. Current through the circuit can be found using the ratio of the voltage of the source to the impedance of the circuit. These all may help you to solve this question.

Complete answer:
As it is mentioned in the question that the voltage across the inductor and the capacitor are equal, we can write that,
${{V}_{1}}={{V}_{2}}$
The voltage across the capacitor can be found by the equation,
${{V}_{2}}=I{{X}_{C}}$
Where $I$ be the current and ${{X}_{C}}$be the capacitive reactance.
The voltage across the inductor will be written as,
${{V}_{1}}=I{{X}_{L}}$
Where ${{X}_{L}}$be the inductive reactance.
As the voltages are equal we can write that,

& I{{X}_{L}}=I{{X}_{C}} \\\ & \Rightarrow {{X}_{L}}={{X}_{C}} \\\ \end{aligned}$$ The frequency of the source can be found using the equation, $$f=\dfrac{1}{2\pi \sqrt{LC}}$$ The value of capacitance and inductance are given in the question, $L=\dfrac{2}{\pi }H$ $C=\dfrac{8}{\pi }\mu F$ Substituting this in the equation will give, $$\begin{aligned} & f=\dfrac{1}{2\pi \sqrt{\dfrac{2}{\pi }\times \dfrac{8}{\pi }\times {{10}^{-6}}}} \\\ & f=\dfrac{1}{2\sqrt{16\times {{10}^{-6}}}} \\\ & \Rightarrow f=\dfrac{{{10}^{3}}}{2\times 4}=125Hz \\\ \end{aligned}$$ Therefore option A is correct and option B is incorrect. The current through the circuit will be the same for every component as they are in series connection. The current through the circuit is, $${{I}_{rms}}=\dfrac{{{V}_{rms}}}{Z}$$ Where $$Z$$be the impedance of the circuit given by the equation, $$Z=\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{C}} \right)}^{2}}}$$ As the circuit is in resonance, $${{X}_{L}}={{X}_{C}}$$ Substituting this in the equation will give, $$\begin{aligned} & Z=\sqrt{{{R}^{2}}+{{\left( 0 \right)}^{2}}} \\\ & \Rightarrow Z=R \\\ \end{aligned}$$ The voltage of the source and resistance are given as, $$\begin{aligned} & {{V}_{rms}}=200V \\\ & R=100\Omega \\\ \end{aligned}$$ Substituting this in the equation, $$\begin{aligned} & {{I}_{rms}}=\dfrac{{{V}_{rms}}}{Z} \\\ & \Rightarrow {{I}_{rms}}=\dfrac{200}{100}=2A \\\ \end{aligned}$$ Therefore the option C is also correct. The voltage across inductor is found by the equation, $$\begin{aligned} & {{V}_{1}}={{I}_{rms}}\times {{X}_{L}} \\\ & \Rightarrow {{V}_{1}}={{I}_{rms}}\times \left( \omega L \right) \\\ & \Rightarrow {{V}_{1}}={{I}_{rms}}\times \left( 2\pi fL \right) \\\ \end{aligned}$$ Substituting the values in it will give, $${{V}_{1}}=2\times \dfrac{2}{\pi }\times 2\times \pi \times 125=1000V$$ As the voltage across inductor and capacitor are same, $${{V}_{2}}={{V}_{1}}=1000V$$ Therefore option D is also correct. **We can conclude that option A, C, D are correct.** **Note:** The LCR series circuit is also known as a resonance circuit. The impedance is very low at resonance. Therefore the current will be high. The high value of current at resonance develops very high values of voltage across the inductor and capacitor.