Question

In the figure shown neglecting friction and mass of pulley what is the acceleration of mass $B$.

A. $\dfrac{g}{3}$
B. $\dfrac{{5g}}{2}$
C. $g$
D. $\dfrac{{2g}}{5}$

Answer 1

In this problem we need to find the acceleration of the block $B$ which is having the mass $m$ in terms of acceleration due to gravity by considering the friction and mass of the pulley as zero. The tension needs to be marked in the given pulley systems. We know that the tensions are the pulling force whose direction is always away from the load as shown in the figure below. The given pulley system consists of one fixed pulley and one movable pulley.

Complete step by step answer:

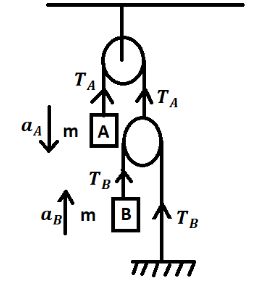
$2{a_A} = {a_B}$ ………. $\left( 1 \right)$
From block $A$ with the mass $m$
$mg - {T_A} = m{a_A}$
On simplifying the above equation we get,
$mg = m{a_A} + {T_A}$ ……….. $\left( 2 \right)$
From block $B$ with the mass $m$
${T_B} - mg = m{a_B}$ ……… $\left( 3 \right)$
Substituting equation $\left( 1 \right)$ in equation $\left( 3 \right)$ we get
${T_B} - mg = m\left( {2{a_B}} \right)$
On simplifying the above equation
${T_B} - mg = 2m{a_B}$
Multiply both sides by$2$, we can write the above equation as
$2{T_B} - 2mg = 4m{a_B}$

On further simplification
$2mg = 2{T_B} - 4m{a_B}$……….. $\left( 4 \right)$
Given that mass of the pulley is neglected
We have, ${T_A} = 2{T_B}$ ………..$\left( 5 \right)$
On subtracting equation $\left( 2 \right)$ and equation $\left( 5 \right)$ we get,
$2mg - mg = 2{T_B} - 4m{a_A} - m{a_A} - {T_A}$ ……..$\left( 6 \right)$
From equation $\left( 5 \right)$, ${T_A} = 2{T_B}$ , equation $\left( 6 \right)$ becomes
$mg = 2{T_B} - 4m{a_A} - m{a_A} - 2{T_B}$
Therefore on further simplification, we can write above equation as
$mg = - 5m{a_A}$
$\Rightarrow {a_A} = \dfrac{g}{5}$ ………..$\left( 7 \right)$
We know that, ${a_B} = 2{a_A}$
Substituting equation $\left( 7 \right)$ in above equation, we get
$\therefore {a_B} = \dfrac{{2g}}{5}$

Hence, option D is correct.

Note: Single fixed pulley and single movable pulley are important pulleys which are used in mechanics. The ideal single fixed pulley has mechanical advantage of $1$ whereas ideal movable pulley has mechanical advantage of 2. The fixed pulley was used to change the direction of the effort only.