Question
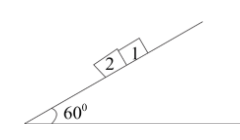
Question: In the figure shown if the friction coefficient of the block \(1\) and \(2\) with the inclined plane...
In the figure shown if the friction coefficient of the block 1 and 2 with the inclined plane is μ1=0.5and μ2=0.4 respectively, then find out the correct statement.
(a) Both blocks will move together
(b) Both blocks will move separately
(c) There is a non-zero contact force between two blocks
(d) None of these
Solution
Hint So to solve this type of problem it is necessary to draw the free fall diagram and in this question, we will consider both the blocks are independent and then we will find the acceleration for both the blocks by using the formulaa=gsinθ−μgcosθ.
Formula used
Acceleration for the block will be
a=gsinθ−μgcosθ
Here,
a, will be the acceleration of the block
g, will be the acceleration due to gravity
Complete Step by Step Solution
Let's consider the two blocks 1 and2, both are independent. Since the blocks are independent so their acceleration will also be independent for both of the blocks.
Acceleration for block1:
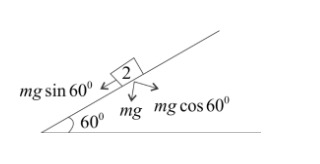
As we know the formula,
a1=gsinθ−μ1gcosθ
Now substitute the values, we get
⇒g[23−21×21]
On solving the above equation, we get
⇒g[423−1]
Therefore, g[423−1] will be the acceleration for the first block.
Similarly,
Acceleration for block2:
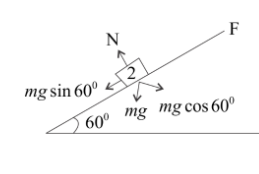
As we know the formula,
a2=gsinθ−μ2gcosθ
Now substitute the values, we get
⇒g[23−52×21]
On solving the above equation, we get
⇒g[53−2]
Therefore, g[53−2] will be the acceleration for the second block.
So, we see that the acceleration a2is greater than the acceleration of a1
Therefore, we can say that both the blocks will move separately.
Hence the option Bwill be correct.
Note Acceleration is positive in the “down” direction, where “down” is where the nearest big source of gravity is.
In physics, acceleration is usually expressed as a vector, i.e. a direction and a magnitude. A magnitude is an absolute value, hence always positive.
We could say the object is accelerating negatively in the “up” direction but that’s a muddled way of looking at things. Direction-and-magnitude makes more sense.
