Solveeit Logo
Login

Question

Question: \- In the figure shown, if the diode forward voltage drops is 0.2V, the voltage difference between A...

- In the figure shown, if the diode forward voltage drops is 0.2V, the voltage difference between A and B is

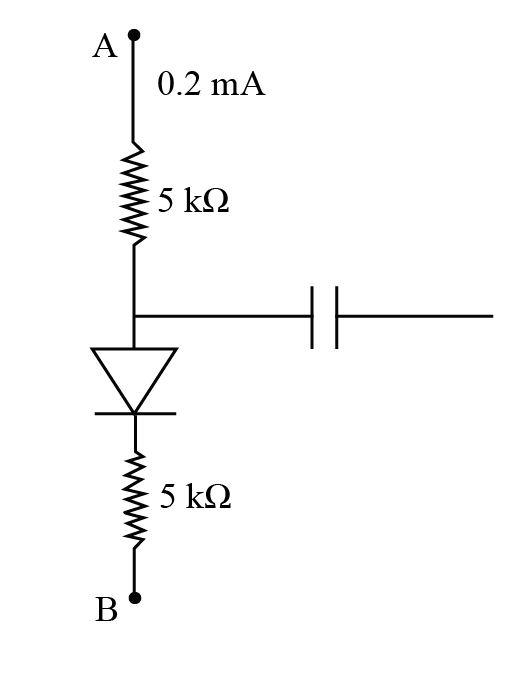
A. 1.3  V1.3\;{\rm{V}}
B. 2.2  V2.2\;{\rm{V}}
C. 0.5  V0.5\;{\rm{V}}
D. 00

Explanation

Solution

This question is based on the Diode. So, we have to know the term diode. Diode is an electronic device that is used to provide an electric current to move in forward direction, and it blocks in the reverse direction. We have to also know the term potential difference. The potential difference is the difference in potential between two points that show the work associated or the energy liberated in transferring a unit amount of electricity from one to another point. By applying Kirchhoff’s voltage law, we can calculate the potential difference between two points A and B.

Complete step by step answer:
Given: The voltage drop across the diode is Vd=0.2  V{V_d} = 0.2\;{\rm{V}}, the current in the circuit is 0.2  mA0.2\;{\rm{mA}} and resistance of the resistor is R=  5  kΩR = \;5\;{\rm{k\Omega }}.

To calculate the potential difference between two points, we have to use the following method.
VAB=IR+Vd+IR{V_{AB}} = IR + {V_d} + IR
Since, there are two resistances so we write IRIR two times.

Now, in a given circuit there are two resistances and a battery.
So, the potential between the two points A and B is,
VAB=IR+Vd+IR   ⟹  VAB=(0.2×10−3)(5×103)+0.2+(0.2×10−3)(5×103)   ⟹  VAB=2.2  Volts {V_{AB}} = IR + {V_d} + IR\\\ \implies {V_{AB}} = \left( {0.2 \times {{10}^{ - 3}}} \right)\left( {5 \times {{10}^3}} \right) + 0.2 + (0.2 \times {10^{ - 3}})(5 \times {10^3})\\\ \implies {V_{AB}} = 2.2\;{\rm{Volts}}
Therefore, the potential between the two points A and B is 2.2  Volts2.2\;{\rm{Volts}}.

Thus, the correct option is B.

Note:
In this question, the students must have the knowledge of potential difference and knowledge of the term diode. This question can alternatively be solved by Kirchhoff's voltage law. Kirchhoff’s gives two laws, first current law and voltage law. Kirchhoff’s current law states that the summation of all the current in the circuit is equal to zero. And Kirchhoff’s voltage law states that the summation of all the voltage in the circuit is equal to zero.