Question
Question: In the figure shown for gives values of $R_1$ and $R_2$ the balance point for Jockey is at 40 cm fro...
In the figure shown for gives values of R1 and R2 the balance point for Jockey is at 40 cm from A. When R2 is shunted by a resistance of 10 Ω, balance shifts to 50 cm. R1 and R2 are (AB = 1m)
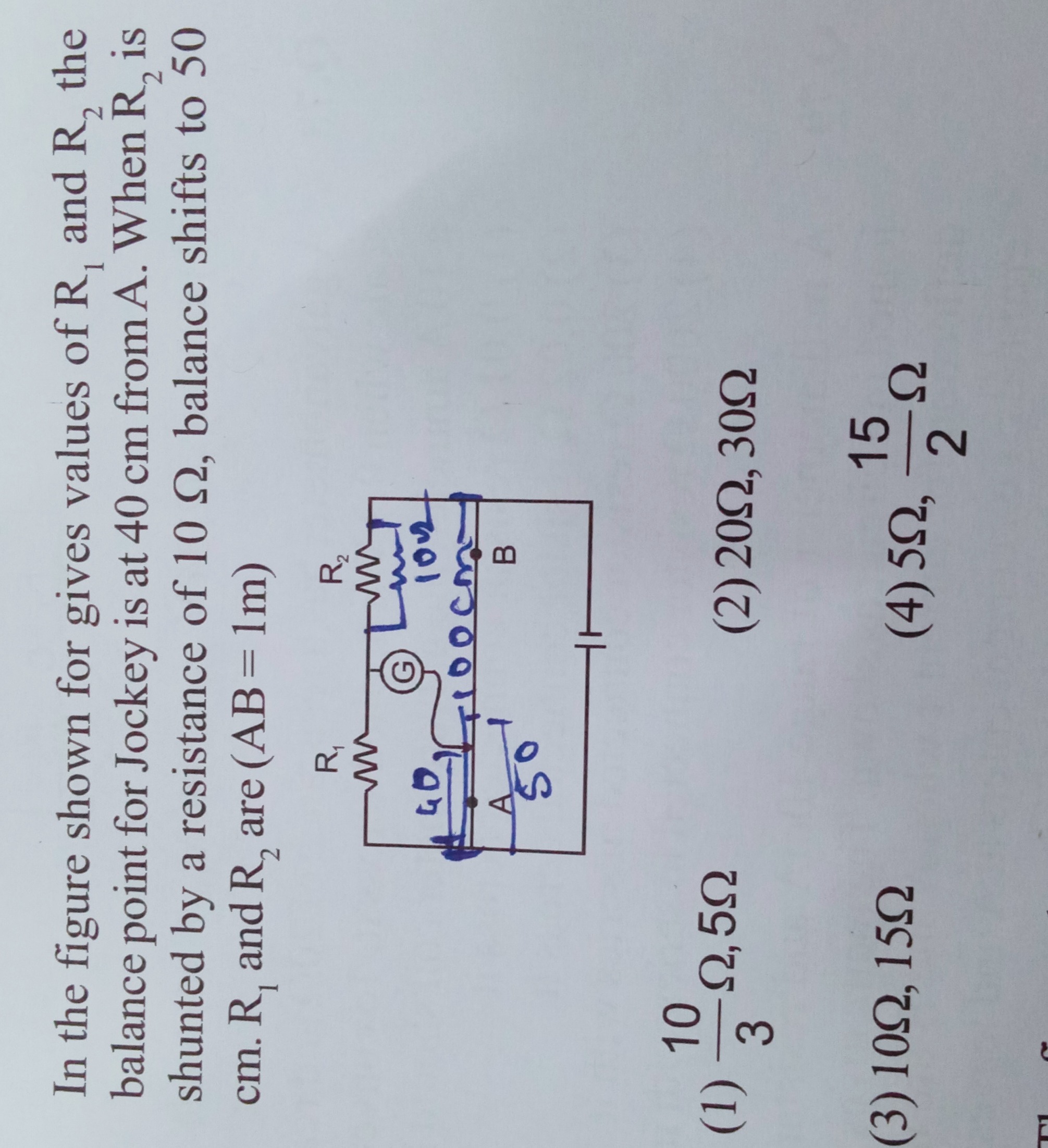
310Ω,5Ω
20Ω, 30Ω
10Ω, 15Ω
5Ω, 215Ω
310Ω,5Ω
Solution
The problem describes a meter bridge experiment. The balance condition for a meter bridge is given by R2R1=100−ll, where R1 is the resistance in the left gap, R2 is the resistance in the right gap, and l is the distance of the balance point from the left end (A) of the wire in cm. The total length of the wire is 100 cm (1 m).
In the first case, the balance point is at 40 cm from A. So, l1=40 cm. The resistance in the left gap is R1 and in the right gap is R2. Applying the balance condition: R2R1=100−4040=6040=32 This gives us the first equation: 3R1=2R2.
In the second case, R2 is shunted by a resistance of 10 Ω. When a resistance Rs is shunted with R2, the equivalent resistance is given by the parallel combination formula: R2,eq=R2+RsR2×Rs. Here, Rs=10Ω. So, R2,eq=R2+1010R2. The balance point shifts to 50 cm from A. So, l2=50 cm. The resistance in the left gap is still R1, and in the right gap is R2,eq. Applying the balance condition: R2,eqR1=100−5050=5050=1 This gives us the second equation: R1=R2,eq.
Substitute the expression for R2,eq into the second equation: R1=R2+1010R2.
Now we have a system of two equations:
- 3R1=2R2⟹R1=32R2
- R1=R2+1010R2
Substitute the expression for R1 from equation (1) into equation (2): 32R2=R2+1010R2
Since R2 is a resistance, it cannot be zero. We can divide both sides by R2: 32=R2+1010
Now, solve for R2: 2(R2+10)=3×10 2R2+20=30 2R2=30−20 2R2=10 R2=5Ω
Now substitute the value of R2 into the expression for R1: R1=32R2=32×5=310Ω
Thus, R1=310Ω and R2=5Ω.
