Question

In the figure shown find the equivalent capacitance between terminals $A$ and $B$ . The letters have their usual meaning. Capacitance is $\dfrac{{x{\varepsilon _o}A}}{{10d}}$. Then $x$ is ?

Answer 1

This question utilizes the concept of capacitance and electric circuits. We can easily find the total capacitance by first separating the two capacitors and then using the capacitor formula to find the total capacitance

Formulae used:
$C = \dfrac{{{\varepsilon _o}A}}{d}$
where $C$ is the capacitance of the parallel plate capacitor, ${\varepsilon _o}$ is the absolute permittivity of the dielectric material being used, $A$ is the area of the plate of the capacitor and $d$ is the distance between the two plates.
When a dielectric with dielectric constant $\kappa$ is introduced in a system, the capacitance changes to $C = \dfrac{{\kappa {\varepsilon _o}A}}{d}$.

Complete step by step answer:
We can bifurcate the complex capacitor into two parts like in the given figure.

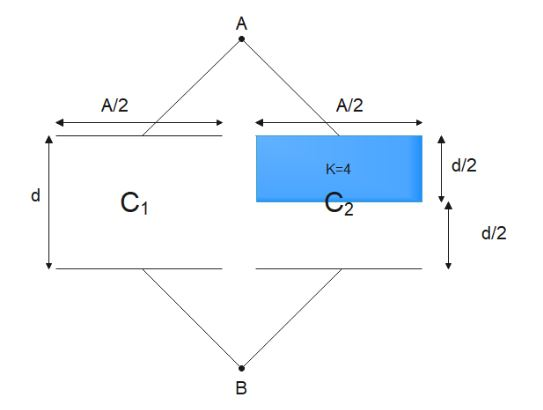
We can see that the two capacitors are in parallel configuration to each other.Now, we find the capacitance of each capacitor individually. For ${C_1}$ , we have

\Rightarrow {C_1} = \dfrac{{{\varepsilon _o}A}}{{2d}} \\\ $$ For ${C_2}$ , we divide the capacitor into two individual capacitors connected in series and label them as ${C_3}$ and ${C_4}$.  Now, for ${C_3}$ $\Rightarrow {C_3} = \dfrac{{\kappa {\varepsilon _o}\dfrac{A}{2}}}{{\dfrac{d}{2}}} \\\ \Rightarrow {C_3} = \dfrac{{\kappa {\varepsilon _o}A}}{d} \\\ $ And for ${C_4}$ $\Rightarrow {C_4} = \dfrac{{{\varepsilon _o}\dfrac{A}{2}}}{{\dfrac{d}{2}}} \\\ \Rightarrow {C_4} = \dfrac{{{\varepsilon _o}A}}{d} \\\ $ Now, since they are in series, we have $ \Rightarrow \dfrac{1}{{{C_2}}} = \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}} \\\ \Rightarrow \dfrac{1}{{{C_2}}} = \dfrac{d}{{\kappa {\varepsilon _o}A}} + \dfrac{d}{{{\varepsilon _o}A}} \\\ \Rightarrow \dfrac{1}{{{C_2}}} = \dfrac{{d + \kappa d}}{{\kappa {\varepsilon _o}A}} \\\ \Rightarrow {C_2} = \dfrac{{k{\varepsilon _o}A}}{{d + \kappa d}} \\\ $ We know from the question that $\kappa = 4$. Thus, $ \Rightarrow {C_2} = \dfrac{{4{\varepsilon _o}A}}{{5d}}$ Now, since ${C_1}$ and ${C_2}$ are in parallel, we get $\Rightarrow C = {C_1} + {C_2} \\\ \Rightarrow C = \dfrac{{{\varepsilon _o}A}}{{2d}} + \dfrac{{4{\varepsilon _o}A}}{{5d}} \\\ \Rightarrow C = \dfrac{{5{\varepsilon _o}A + 8{\varepsilon _o}A}}{{10d}} \\\ \therefore C = \dfrac{{13{\varepsilon _o}A}}{{10d}} $ **Therefore, the value of $x$ is $13$.** **Note:** Many students might commit the mistake of solving the whole capacitor as a single entity. This would result in silly mistakes and might even fetch you the wrong answer.Hence, whenever you get a complex question, first break it down into smaller pieces and then solve it.