Question
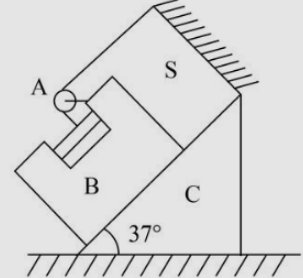
Question: In the figure shown C is a fixed wedge. A block B is kept on the inclined surface of the wedge C. An...
In the figure shown C is a fixed wedge. A block B is kept on the inclined surface of the wedge C. Another block A is inserted in a slot in the block B as shown in figure. A light inextensible string passes over a light pulley which is fixed to the block B through a light rod. One end of the string is fixed and the other end of the string is fixed to A.S is a fixed support on the wedge. All the surfaces are smooth. Masses of A and B are the same. Then the magnitude of acceleration of A is 3xm/s2. Then x is (sin37∘=3/5).
Solution
The above problem can be resolved by applying the equilibrium condition for the forces acting on the block A and block B. The block A and block B are attached with a string, on which the tension force can be applied as the reaction force. Moreover, the equations for the forces at A and B compared to calculate the value of net acceleration at A
Complete step by step answer:
Apply the string constraint relation to relation between the acceleration of the block A and block B as,
aA+aB=0
Here, aA and aB are the acceleration of block A and B. As, the magnitude of acceleration for the block A and B are same then, aA=aB=a.
Now, balance the forces for block B as,
2mgsinθ−T=2ma.............................(1)
Here, m is the mass of block B and its value is given equal to mass of block A, g is the gravitational acceleration and θ is the wedge angle.
Now, write the equations of forces for the block A as,
T−mgcosθ=ma.....................................(2)
Substitute the value of equation 2 in 1 as,
Further solving the above equation as,
3T=2mgsin37∘+2mgcos37∘ ⇒3T=2mg×(53)+2mg×(54) ⇒T=514mgThe acceleration of the block A is,
T - mg\cos \theta = ma\\\ \Rightarrow \left( {\dfrac{{14mg}}{{15}}} \right) - mg\left( {\dfrac{4}{5}} \right) = ma\\\ \Rightarrow a = \dfrac{4}{3}\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$$ As, the magnitude of acceleration for the block A and B are the same. Therefore, the net acceleration is,{a_{net}} = \sqrt {a_A^2 + a_B^2} \\
\Rightarrow{a_{net}} = \sqrt {{a^2} + {a^2}} \\
\Rightarrow{a_{net}} = \sqrt {{{\left( {\dfrac{4}{3}} \right)}^2} + {{\left( {\dfrac{4}{3}} \right)}^2}} \\
\therefore{a_{net}} = \dfrac{{\sqrt {32} }}{3};{\rm{m/}}{{\rm{s}}^{\rm{2}}}
