Question
Question: In the figure shown, after the switch \('S'\) is turned from the position \('A'\) to position \('B'\...
In the figure shown, after the switch ′S′ is turned from the position ′A′ to position ′B′ , the energy dissipated in the circuit in terms of capacitance ′C′ and total charge ′Q′ is:
(A) 83CQ2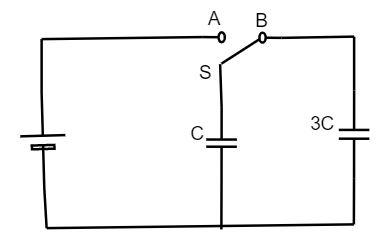
(B) 43CQ2
(C) 81CQ2
(D) 85CQ2
Solution
Use the formula of the energy stored in the capacitor and find its answer. Use the formula of the energy liberated and substitute the value of the equivalent capacitance to find its answer. Subtract both the answer to find the value of the energy dissipated to the surrounding.
Formula used:
(1) The formula of the energy stored in the capacitor is given by
U=21CV2
Where U is the energy stored in the capacitor, C is the capacitance and V is the voltage of the capacitor.
(2) The energy dissipated in the circuit is given by
V=2CeqCV2
Where V is the energy dissipated to the surrounding and Ceq is the equivalent capacitance of the circuit.
Complete step by step solution:
From the given circuit diagram, the capacitance of the C and 3C are connected parallel to each other. A and B are two switch connections.
Using the formula of the energy stored we get
U=21CV2 ……………………….(1)
Substitute that C=VQ in the above step, we get
U=2CQ2 ……………………..(2)
Using the formula of the energy dissipated to the surrounding, we get
V=2CeqCV2 ……………………….(3)
From the circuit, the equivalent capacitance of the circuit is calculated as follows.
⇒Ceq=1+3=4
Substitute this in the equation (2), we get
⇒V=2×4CV2=8CV2 …………….(4)
The change in the energy is obtained by subtracting the (4) and (1),
⇒ΔE=2CV2−8CV2=83CV2
Substituting the equation (2) in the above step, we get
⇒ΔE=83CQ2
Thus the option (A) is correct.
Note: The main work of the capacitance is to collect the energy and to store it. But there will be some loss of the energy and its mainly due to the voltage drop across the capacitor. If the voltage drop is high, then the power dissipation in the capacitor will also be high.
