Question
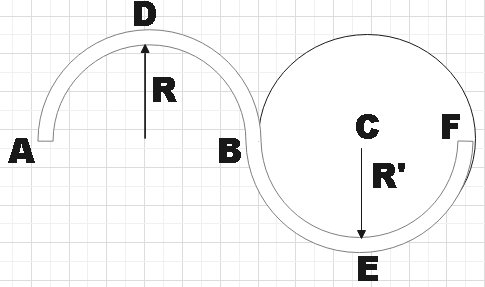
Question: In the figure shown ADB and BEF are two fixed smooth circular paths of radius R and R’ respectively....
In the figure shown ADB and BEF are two fixed smooth circular paths of radius R and R’ respectively. A block of mass m enters in the tube ADB through point A with minimum velocity to reach point B. From there it moves on other circular path BEF and it is just able to complete the circle
The ratio of radius of two circular paths ADB and BEF is
A. R′R=32
B. R′R=23
C. R′R=52
D. R′R=25
Solution
You could recall the condition to be satisfied so as the block will complete its motion around the circle. This would be the velocity at the minimum point. Now, you could apply law of conservation of energy on the system and then rearrange the terms and hence get the required ratio.
Complete step by step solution:
In the question, we are given two fixed smooth circular paths ADB and BEF of radii R and R’. A block of mass m enters ADB through A with certain minimum velocity to reach B and then moves to BEF and hence completes the circle. We are asked to find the ratio of radii of the two circular paths from the given information.
Let the block have a minimum velocity vA at point A and the kinetic energy will be transferred to potential energy on reaching point D. So,
21mvA2=mgR
⇒vA=2gR ……………………………….. (1)
Now, for the block to complete its motion around the other circle, we have this condition for velocity at the minimum point E,
vE=5gR′ ………………………………………. (2)
Now, from law of conservation of energy we have,
mg(R+R′)=21mvE2
Substituting (2) we get,
mg(R+R′)=21m(5gR′)
⇒R+R′=25R′
⇒R=25R′−2R′=23R′
∴R′R=23
Therefore, we found the required ratio to be R′R=23
Hence, option B is found to be the correct answer.
Note: While solving we have used the law of conservation of energy. This law states that the total energy of an isolated system remains constant or in other words conserved over time. Another way to state this law is ‘energy can neither be created nor be destroyed but can be transformed from one form to another.
