Question

In the figure shown, ABC is a uniform wire. If the center of mass of wire lies vertically below point A, then the ratio of ab, bc​ is close to:

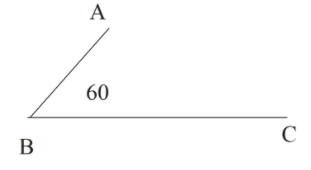
A) 1.85
B) 1.5
C) 1.37
D) 3

Answer 1

It is given that the center of mass lies below vertically A. Let us find the distance of the center of mass of the AB from point b. Assume the linear mass of the given wire and find the mass of two wires in terms of linear mass density. Next, apply the center of mass formula and find the ratio.
Formulas used:
${{x}_{com}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$

Complete step-by-step solution:
Let us first find the distance of the centre of mass of the system from point B. As the centre of mass lies on vertically below A,
The distance of centre of mass from point B will be,
$\begin{aligned} & {{x}_{com}}={{l}_{1}}\cos {{60}^{0}} \\\ & {{x}_{com}}=\dfrac{{{l}_{1}}}{2} \\\ \end{aligned}$
Let us assume the linear mass density as $\lambda =\dfrac{m}{l}$
Now, the centre of mass of wire BC lies at the centre, so, distance will be $\dfrac{{{l}_{2}}}{2}$
Substituting in the formula,
We get,
$\begin{aligned} & {{x}_{com}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}} \\\ & \Rightarrow \dfrac{{{l}_{1}}}{2}=\dfrac{\lambda {{l}_{1}}\times \dfrac{{{l}_{1}}}{4}+\lambda {{l}_{2}}\times \dfrac{{{l}_{2}}}{2}}{\lambda ({{l}_{1}}+{{l}_{2}})} \\\ & \Rightarrow {{l}_{1}}({{l}_{1}}+{{l}_{2}})=\dfrac{{{l}_{1}}^{2}}{2}+{{l}_{2}}^{2} \\\ & \Rightarrow 2{{l}_{2}}^{2}-2{{l}_{1}}{{l}_{2}}-{{l}_{1}}^{2}=0 \\\ \end{aligned}$
On solving the equation, we get,
$\begin{aligned} & {{l}_{2}}=\dfrac{{{l}_{1}}\pm \sqrt{3}{{l}_{1}}}{2} \\\ & \Rightarrow \dfrac{{{l}_{2}}}{{{l}_{1}}}=\dfrac{1+\sqrt{3}}{2} \\\ & \Rightarrow \dfrac{{{l}_{1}}}{{{l}_{2}}}=1.366 \\\ \end{aligned}$
Therefore, the correct option is option C.
Additional information:
The Centre of the mass of a body or system of a particle is defined as, a point at which the whole of the mass of the body or all the masses of a system of particles appears to be concentrated. When we are studying the dynamics of the motion of the system of a particle as a whole, then we need not bother about the dynamics of individual particles of the system. But only focus on the dynamic of a unique point corresponding to that system. The motion of this unique point is identical to the motion of a single particle whose mass is equal to the sum of all individual particles of the system and the resultant of all the forces exerted on all the particles of the system by surrounding bodies (or) action of a field of force is exerted directly to that particle. This point is called the center of mass of the system of particles. The concept of center of mass (COM) is useful in analyzing the complicated motion of the system of objects, particularly When two and more objects collide or an object explodes into fragments.

Note: In the above question, the center of mass of the second wire is positioned at half the length of the wire. For the first wire, the center of wire lies vertically below point A, therefore the x-coordinate of the total length is taken as the position of center of mass of the system.