Question
Question: In the figure shown, a ring A is initially rolling without sliding with a velocity v, on the horizon...
In the figure shown, a ring A is initially rolling without sliding with a velocity v, on the horizontal surface of the body B (of the same mass as A). All the surfaces are smooth. B has no initial velocity. What will be the maximum height reached by A on B?
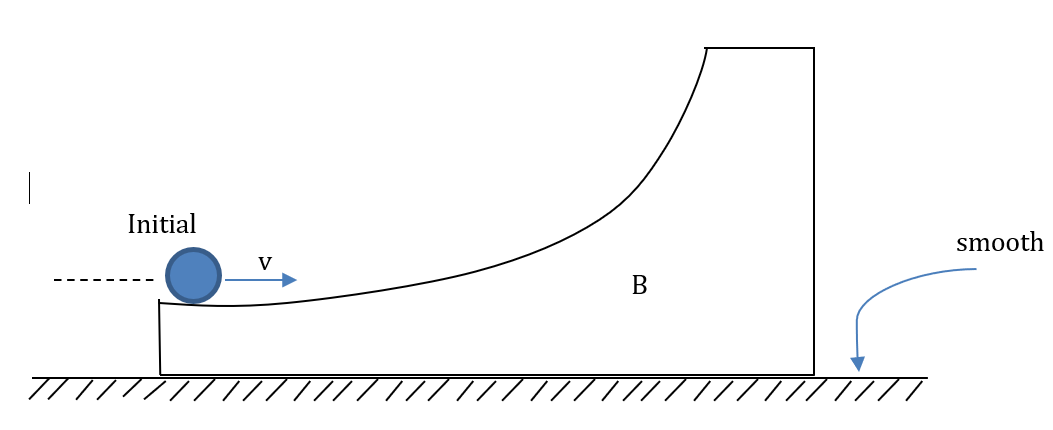
A.4g3v2B.4gv2C.2gv2D.3gv2
Solution
Hint: Use the law of conservation of total mechanical energy and the conservation of the total momentum to solve the problem. Do consider the rotational and translational Kinetic energy while using the conservation law.
Complete step-by-step answer:
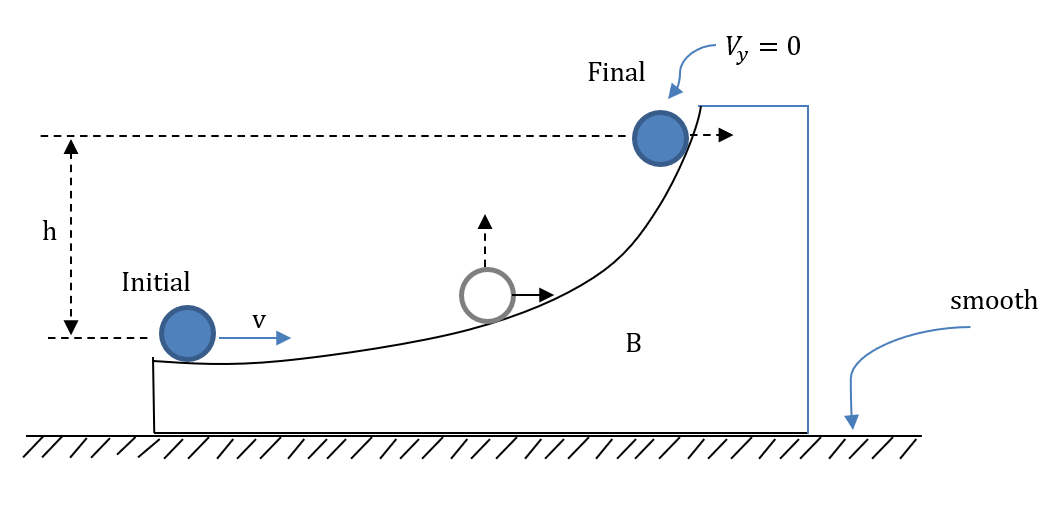
The given initial value of the velocity is v.When the ring is at the maximum height, the wedge and the ring have the same horizontal component of velocity. As all the surfaces are smooth, in the absence of friction between the ring and the wedge surface, the angular velocity of the ring remains constant.
The law conservation of the total mechanical energy says that total initial mechanical energy is the same as the total final mechanical energy and we get as
Rotational Kinetic energy is given by : KErot=2Iω2
Translational Kinetic energy is given by : KEtrans=2mv2
Total initial mechanical energy as : TMEinit=21mv2+21Iω2
Similarly, the final total mechanical energy becomes TMEfinal=21mvI2+21Iω2+21mvI2+mghwhere vI is the final common velocity of the bodies.
Using the conservation of momentum we get the initial momentum is equal to the final momentum we get : mv+0=(2m)vI
vI=2v so the substitution of this will give us
21mv2+21Iω2=21m(2v)2+21Iω2+21(2v)2+mgh
We get the value of h=4gv2
So using the conservation of the total mechanical energy we are able to find the value of h=4gv2, so B is correct here.
Note: The most common mistake that one can do in this kind of question with frictional surfaces is that we take the final value of rotational kinetic energy as zero and hence we get an error. Due to the frictionless surfaces, the value of rotational kinetic energy is the same .
