Question
Question: In the figure shown, a potential of \[ + 12V\] is given to point \(A\) and point \(B\) is earthed. W...
In the figure shown, a potential of +12V is given to point A and point B is earthed. What is the potential at point P ?
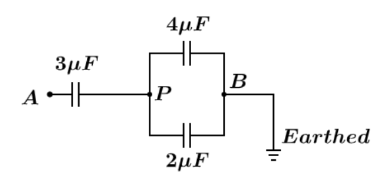
Solution
In order to find Potential at point P, we need to find the actual potential difference between Point A and point P which is the potential across the capacitor of capacitance 3μF . Then we will use the general potential difference formula which is VAP=VA−VP .
Formula Used:
In case when two capacitors of capacitance C1 and C2 are connected in parallel combination the net capacitance is calculated as Cnet=C1+C2 while, if two capacitors are connected in series ten their net capacitance is calculated as Cnet1=C11+C21 .
Complete step by step answer:
Firstly, let us find the equivalent capacitance between points A and B. Since, the capacitors of capacitance 2μF and 4μF are connected in parallel with each other so, their resultant capacitance is calculated using formula Cnet=C1+C2 so, and we have
C2,4=2+4
⇒C2,4=6μF
Now, this net capacitance of C2,4=6μF is connected in series with the capacitor of capacitance 3μF so, the net capacitance between point A and B can be calculated by using formula Cnet1=C11+C21
so, we have
C3,61=31+61
⇒C3,61=189
⇒C3,6=2μF
The net capacitance between point A and point B is 2μF .
Now, let Qnet be the charge on this net capacitance and the potential at point is given as VA=+12V and point B is earthed so VB=0 using the formula Q=CV we can write this for net capacitance of 2μF as
Qnet=CnetVAB
⇒Qnet=2(VA−VB)→(i)
Now, since capacitor of capacitance 3μF and capacitor of capacitance C2,4=6μF are connected in series then, total charge Qnet will distribute same across both the capacitors, hence we have the charge stored on 3μF capacitor is Qnet and the potential difference across 3μF is denoted as VAP so we can write as:
Qnet=CVAP
⇒Qnet=3(VA−VP)→(ii)
Compare the equations (i)and(ii) we get,
2(VA−VB)=3(VA−VP)
And we have, VA=+12V and VB=0 hence,
3VP=12
∴VP=4V
Hence, the potential at point P is 4V.
Note: It should be remembered that, when two capacitors are connected in series, the same charge flows across them while when two capacitors are connected in parallel, voltage across both the capacitors are the same. When any point of the electrical circuit is grounded the voltage or potential at the point becomes zero.
