Question

In the figure shown, a point object $O$ is placed in air. A spherical boundary separates two media. $AB$ is the principal axis. The refractive index above $AB$ is $1.6$ and below $AB$ is $2.0$ The separation between the images formed due to refraction at spherical surface is

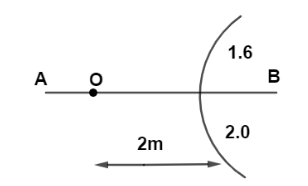
A. $12m$
B. $20m$
C. $14m$
D. $10m$

Answer 1

In order to solve this question we need to understand the type of lenses and spherical surface. So lens are of two types one is concave and other is convex lens. Concave lens is a diverging lens and it diverges a parallel beam of light falling on it such that it appears to come from a point known as focal point. And the convex lens is a converging lens and it converges the parallel beam of light falling on it such that it appears to come from a point known as focal point.

Complete step by step answer:
Let the incident light fall on a spherical surface in medium one whose refractive index is ${\mu _1}$ and it gets refracted at boundary in medium two whose refractive index is given by ${\mu _2}$. We know an image created by half of a spherical surface is equivalent to an image created from a full spherical surface. So using lens formula of refractive index for both upper and lower half we have,
For Upper half, object distance is $u = - 2\,m$
And ${\mu _1} = 1$ , ${\mu _2} = 1.6$

So using relation and assuming Radius to be $R = 1m$. We have,
$\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{R}$
Putting values we get,
$\dfrac{{1.6}}{v} + \dfrac{1}{2} = \dfrac{{1.6 - 1}}{1}$
$\Rightarrow \dfrac{{1.6}}{v} = 0.6 - 0.5$
$\Rightarrow v = \dfrac{{1.6}}{{0.1}}$
$\Rightarrow v = 16\,m$

For lower half we have, object distance is $u = - 2m$
And ${\mu _1} = 1$ , ${\mu _2} = 2.0$
So using relation and assuming Radius to be $R = 1m$
We have, $\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{R}$
Putting values we get,
$\dfrac{{2.0}}{{{v_1}}} + \dfrac{1}{2} = \dfrac{{2.0 - 1}}{1}$
$\Rightarrow \dfrac{2}{{{v_1}}} = 1.0 - 0.5$
$\Rightarrow {v_1} = \dfrac{2}{{0.5}}$
$\therefore {v_1} = 4\,m$
So the difference between two images is $v - {v_1}$. Putting values we get $16 - 4 = 12\,m$.

So the correct answer is A.

Note: It should be remembered that refractive index is a characteristic of the medium and it is equal to sine of angle of incidence to the sine of angle of refraction. Since two mediums have different refractive index, the light speed in two mediums is different and that is why either light bends away or towards the normal upon getting refracted in the second medium.