Question

In the figure shown, a metal rod of length 1m and moving with a velocity of $10m{{s}^{-1}}$ constitutes a closed circuit which is lying in a perpendicular magnetic field of 1T. If $R=10\Omega$, then force necessary to keep the rod moving will be:

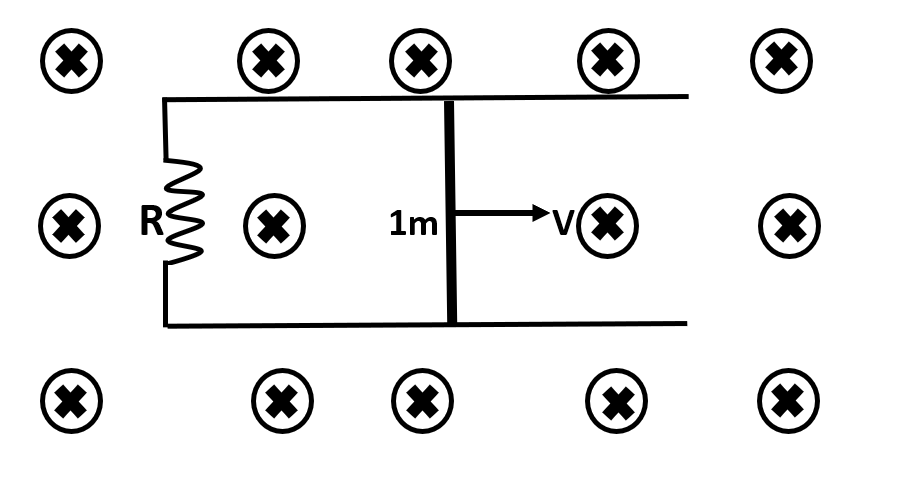
$\begin{aligned} & (A)0.01N \\\ & (B)0.1N \\\ & (C)1.0N \\\ & (D)10N \\\ \end{aligned}$

Answer 1

Since, the rod is moving perpendicular to the magnetic field, a current will be induced in the circuit. This current will be clockwise in direction (along the direction of $\overrightarrow{v}\times \overrightarrow{B}$ ). We will first calculate this current and then calculate the force necessary to keep the rod mobbing that is given by, current multiplied by vector cross-product of length and magnetic field.

Complete answer:
Let the rod move a distance (x) in time (t), then the area (say A) covered by the rod in this time is given by:
$\begin{aligned} & \Rightarrow A=(1\times x){{m}^{2}} \\\ & \Rightarrow A=x{{m}^{2}} \\\ \end{aligned}$
Therefore, the magnetic flux through this area can be written as:
$\begin{aligned} & \Rightarrow {{\phi }_{B}}=\overrightarrow{B}.\overrightarrow{A} \\\ & \Rightarrow {{\phi }_{B}}=(Bx)T{{m}^{2}} \\\ \end{aligned}$
Where, vector B is the magnetic field vector and its magnitude is 1T.
Now, the induced electric potential in the rod is time differential of changing magnetic field, that is:
$\begin{aligned} & \Rightarrow \left| E \right|=\dfrac{d{{\phi }_{B}}}{dt} \\\ & \Rightarrow \left| E \right|=\dfrac{d(Bx)}{dt} \\\ & \Rightarrow \left| E \right|=\dfrac{Bdx}{dt} \\\ & \Rightarrow \left| E \right|=Bv\text{ }\left[ \because \dfrac{dx}{dt}\text{=v} \right] \\\ \end{aligned}$
Now, putting the values of B and v in the above equation, we get:
$\begin{aligned} & \Rightarrow \left| E \right|=1\times 10 \\\ & \Rightarrow \left| E \right|=10V \\\ \end{aligned}$
Hence, the current through the circuit (say I) will be equal to:
$\Rightarrow I=\dfrac{\left| E \right|}{R}$
Putting the values of all the known terms, we get:
$\begin{aligned} & \Rightarrow I=\dfrac{10}{10}A \\\ & \Rightarrow I=1A \\\ \end{aligned}$
Thus, the magnitude of force necessary to keep the rod moving shall be:
$\Rightarrow \left| F \right|=ILB$
$\begin{aligned} & \Rightarrow \left| F \right|=1\times 1\times 1N \\\ & \therefore \left| F \right|=1N \\\ \end{aligned}$
Hence, the magnitude of force necessary to keep the rod moving comes out to be 1N.

Hence, option (C) is the correct option.

Note:
We were interested in finding only the magnitude of electric potential because we had already assigned the current direction in the circuit which is clockwise. This means that the upper part of the rod must be acting as a positive terminal and the lower part as a negative terminal of a battery.