Question

In the figure shown, a circuit contains two identical resistors with resistance $R = 5\Omega$ and an inductance with $L = 2mH$. An ideal battery of $15V$ is connected in the circuit. What will be the current through the battery long after the switch is closed?

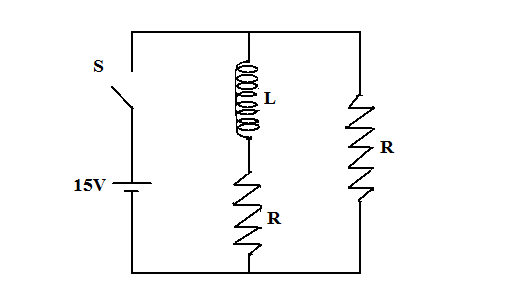
(A) $6A$
(B) $7.5A$
(C) $5.5A$
(D) $3A$

Answer 1

You must know the behaviour of the inductors, resistors and the capacitors after the switch is closed. You must also know that the value of the current and charge depends upon the time they pass in the circuit. Also remember that the inductor will behave as a zero resistance wire after passing a long time in a circuit.

Formula used:
$i = \dfrac{V}{R}$
Where $i$ is the current flowing
$V$ is the voltage difference
$R$ is the resistance

Complete step by step answer:
As we know that the the inductor behaves as a plane wire or a zero resistance wire after it passes a long time in a circuit, for $t \to \infty$
So, after circuit will become like,

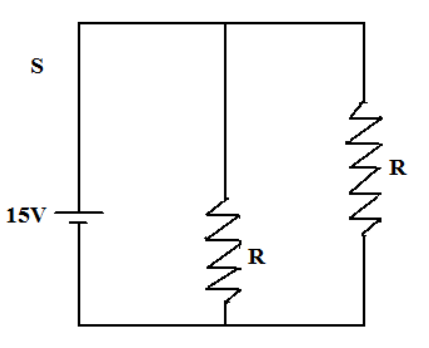
Here, the switch is closed for a long time so the inductor behaves as a zero resistance wire, so we remove the inductor and place a plane wire over there.
Now, we have only two resistance of same value which are connected as parallel to each other, so the ${R_{eq}}$ for this is given by,
${R_{eq}} = \dfrac{R}{2}$
And the voltage of the battery connected is given as,
$V = 15V$
By applying the formula for the current,
$i = \dfrac{V}{{{R_{eq}}}}$
Where $i$ is the current flowing in the circuit
$V$ is the voltage difference across the circuit
${R_{eq}}$ is the equivalent resistance of the circuit
On putting all the values of the variable we have,
$\Rightarrow i = \dfrac{{15 \times 2}}{R}$ {$\therefore$ ${R_{eq}} = \dfrac{R}{2}$ }
We have also given the value of $R$in the question that is,
$R = 5\Omega$
On putting that in the above equation, we get
$\Rightarrow i = \dfrac{{15 \times 2}}{5}$
On further solving, we get the value of current through the battery long after the switch is closed is,
$i = 6A$

Therefore, the correct option is option (A).

Note: The effect of an inductor in a circuit is to oppose changes in current through it by developing a voltage across it proportional to the rate of change of the current. Inductors are used to create magnetic fields in electrical machines for the purpose of energy conversion. For DC current, inductors act as a simple wire but for AC, they oppose the current change in circuits.