Question

In the figure shown A and B are free to move. All the surfaces are smooth. Mass of A is m. Then:

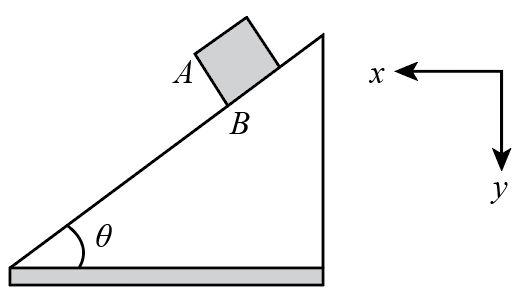
A. the acceleration of A will be more than $g\sin \theta$
B. the acceleration of A will be less than $g\sin \theta$
C. the acceleration of A due to B will be more than $mg\cos \theta$
D. the acceleration of A due to B will be less than $mg\cos \theta$

Answer 1

In this question we have to apply the concepts of kinematics, forces on a body placed on an inclined plane and the concepts of free body diagrams. Using all these concepts we have to find the conditions which support or contradict the options given in the questions and we have to find which of the options are correct.

Complete step by step answer:

We are given in the question that both the bodies A and B are free to move and all the surfaces are smooth. Therefore, we do not have to take friction in consideration.
When the bodies will be released at such a position given in the question, A will slide along the inclined plane and B will move in the right direction as there will be contact force acting on B due to A.
We can easily understand the concepts if we draw the free body diagrams of the body A.

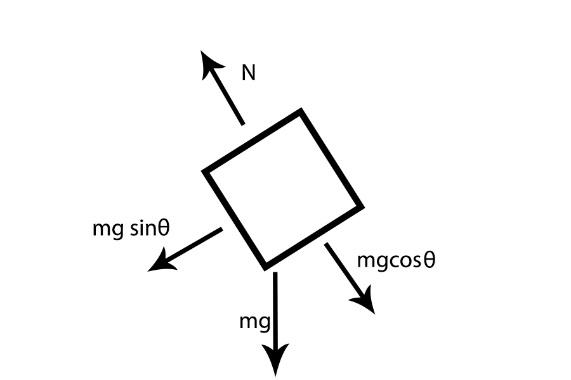
Here above we have resolved the weight of the body into the components in the direction of the plane and perpendicular to the direction of the plane.
If we calculate the acceleration of the body A in the direction of left side we get:
$\begin{array}{l} a = \dfrac{{mg\sin \theta }}{m}\\\ \Rightarrow a = g\sin \theta \end{array}$
Now this is the acceleration if the inclined plane does not move. Since the inclined plane is moving it will also give some acceleration in the same direction hence the acceleration of the body A is slightly more than $g\sin \theta$.
Therefore, the option A, is correct.
Further, if we consider the body B, since it is moving in the right direction, then there must be some force acting on body B due to body a hence if the body A is exerting force in downwards direction then the normal reaction force and the weight are not cancelled but the weight component is more than the normal reaction force, Hence the normal reaction force on A due to B will be less than $mg\cos \theta$.
Therefore, the option D is also correct.

Hence, the correct options are option A and option D.

Note:
While answering such multiple-choice questions where more than one answer is correct, students should check all the possibilities in that question. If a student gets one of the options as the correct answer and leaves the rest of the options unattended then the solution will not be complete.