Question
Question: In the figure, PQ is the diameter of the circle. If \( \angle PQR={{65}^{\circ }} \) , \( \angle RPS...
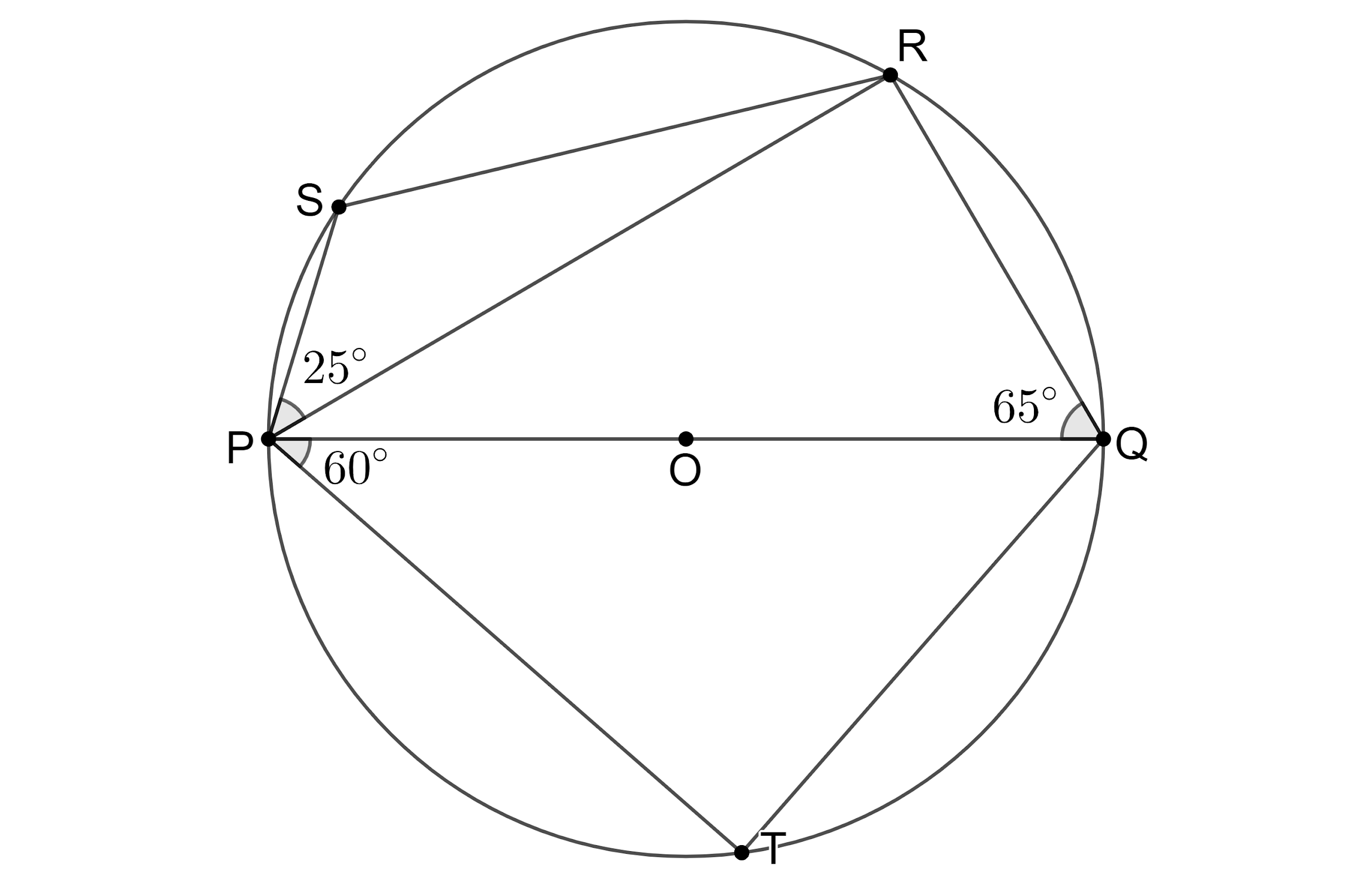
In the figure, PQ is the diameter of the circle. If ∠PQR=65∘ , ∠RPS=25∘ and ∠QPT=60∘ , then find the measure of (i) ∠QPR , (ii) ∠PRS , (iii) ∠PSR and (iv) ∠PQT ?
Solution
We start solving the problem by making use of the fact that angle in a semicircle is 90∘ to find the value of angle ∠QTP . We then make use of the fact that the sum of the angles in a triangle is 180∘ for triangle PQT to find the angle ∠PQT . We then make use of the fact that angle in a semicircle is 90∘ to find the value of angle ∠QRP . We then make use of the fact that the sum of the angles in a triangle is 180∘ for triangle PQR to find the angle ∠QPR . We then make use of the fact that the sum of opposite angles in a concyclic polynomial is 180∘ to find the angle ∠PSR . We then make use of the fact that the sum of the angles in a triangle is 180∘ for triangle PRS to find the angle ∠PRS.
Complete step by step answer:
According to the problem, we are given that PQ is the diameter of the circle. If ∠PQR=65∘ , ∠RPS=25∘ and ∠QPT=60∘ . We need to find the values of the angles (i) ∠QPR , (ii) ∠PRS , (iii) ∠PSR and (iv) ∠PQT .
Let us redraw the given figure,
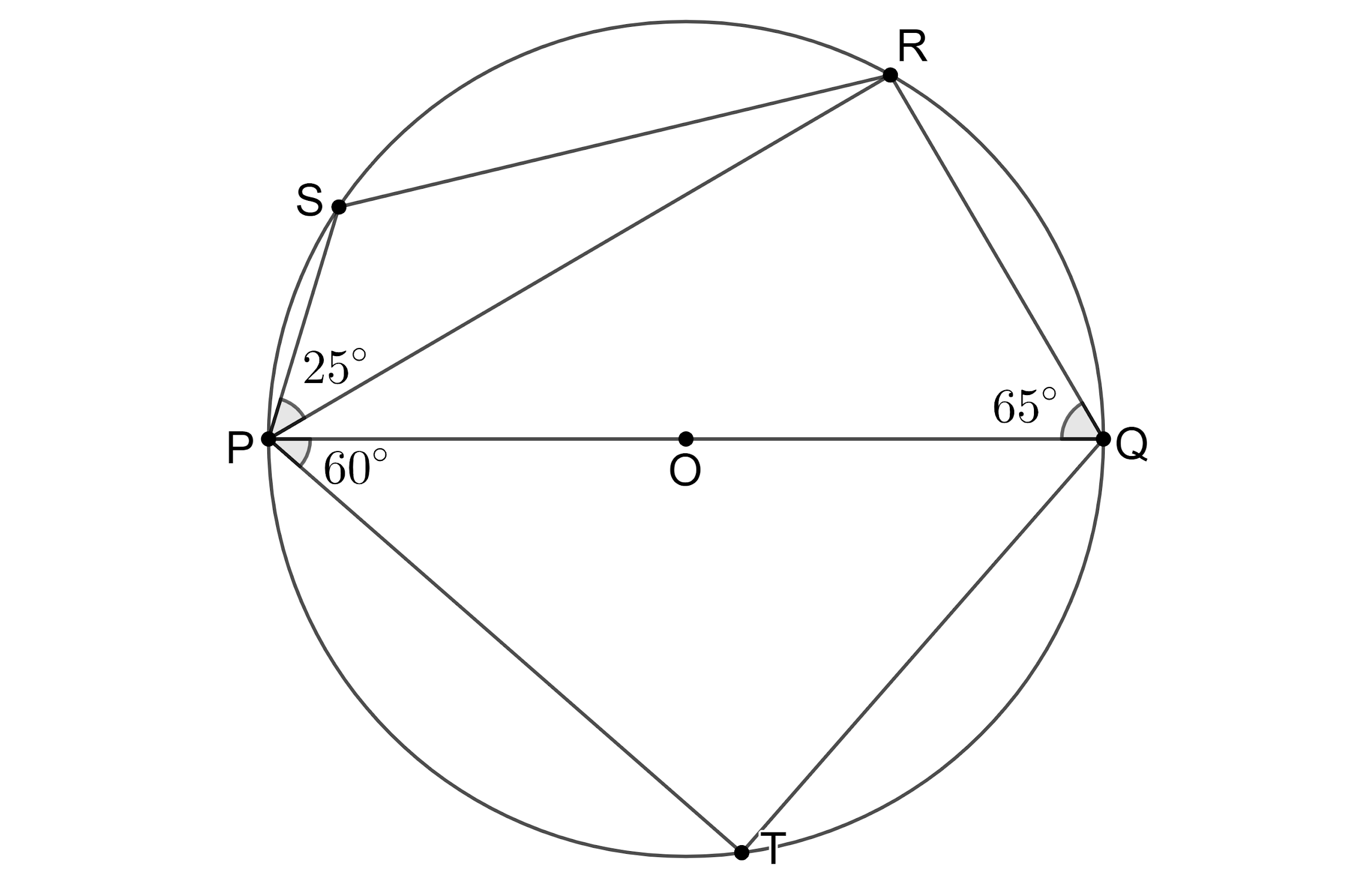
From the figure, we can see that ∠QTP is the angle formed by connecting the ends of the diameter of the circle, which means that the angle ∠QTP is the angle in a semicircle. We know that angle in a semicircle is 90∘ so, we get ∠QTP=90∘ ---(1).
We know that the sum of the angles in a triangle is 180∘.
From the triangle PQT , we have ∠QTP+∠TPQ+∠PQT=180∘ .
From equation (1), we get
⇒60∘+90∘+∠PQT=180∘ .
⇒150∘+∠PQT=180∘ .
⇒∠PQT=30∘ .
From the figure, we can see that ∠QRP is the angle formed by connecting the ends of the diameter of the circle, which means that the angle ∠QRP is the angle in a semicircle. We know that angle in a semicircle is 90∘ , so we get ∠QRP=90∘ ---(2).
We know that the sum of the angles in a triangle is 180∘.
From the triangle PQR , we have ∠PQR+∠QRP+∠QPR=180∘ .
From equation (2), we get
⇒65∘+90∘+∠QPR=180∘ .
⇒155∘+∠QPR=180∘ .
⇒∠QPR=25∘ .
We can see that the points P, Q, R, S form a concyclic quadrilateral. We know that the sum of opposite angles in a concyclic polynomial is 180∘.
So, we have ∠PQR+∠PSR=180∘ .
⇒65∘+∠PSR=180∘ .
⇒∠PSR=115∘ ---(3).
We know that the sum of the angles in a triangle is 180∘.
From triangle PSR , we have ∠PSR+∠PRS+∠RPS=180∘ .
From equation (3), we get
⇒25∘+115∘+∠PRS=180∘ .
⇒140∘+∠PRS=180∘ .
⇒∠PRS=40∘ .
∴ We have found the values of angles ∠QPR , ∠PRS , ∠PSR and ∠PQT as 25∘ , 40∘ , 115∘ and 30∘ .
Note:
We can see that the given problem contains a huge amount of calculations, so we need to perform each step carefully to avoid confusion. We should not confuse angles while using the property of angle in a semi-circle. We should not make calculation mistakes while solving this problem. Whenever we get this type of problem, we should make use of properties of concyclic polygons and angle in a semi-circle to get the required answer.
