Question
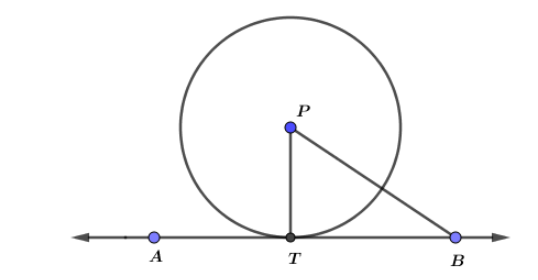
Question: In the figure point P is the centre of the circle and line AB is the tangent to the circle at T. The...
In the figure point P is the centre of the circle and line AB is the tangent to the circle at T. The radius of the circle is 6 cm. Find PB if ∠TPB = 60°.
A. 12 cm
B. 24 cm
C. 8 cm
D. 18 cm
Solution
Here, first using property of tangent to a circle, prove that triangle PTB is a right triangle. As PTB is a right angled triangle, also ∠TPB is given, so we can use trigonometric tools to find the length of PB.
Complete step-by-step answer:
Given that a circle with centre P and radius PT = 6 cm, and AB is a tangent passing through T.
Also given ∠TPB = 60°.
Here, T is the point of contact of tangent and circle.
Since, AB is tangent to the circle, ∠PTB = 90°.
[Property of tangent to a circle: Tangent to a circle is always perpendicular to the point of contact]
In triangle ATB,
∠ATB + ∠TAB + ∠TBP = 180°
[Angle sum property: Angle sum property of a triangle states that sum of all angles of a triangle is 180°]
We have, ∠ATB = 90°, ∠TAB = 60°
Therefore, 90° + 60° + ∠TBP = 180°
150° + ∠TBP = 180°
∠TBP =180° − 150° = 30°
Now, again in triangle ATB,
sin ∠TBP = PBPT
sin 30° = PB6
21=PB6
Cross multiplying
PB = 12 cm
Therefore, the length of PB is 12 cm.
Hence, option (A) is correct.
Note:
In these types of questions, if you find a right angled triangle, with one side and one standard angle like 30°, 45°, 60° are given, then always use a trigonometric method to find the unknown side.
As values of trigonometric tools like sine, cos, tan etc are defined for some angles like 30°, 45°, 60° can be easily used.
