Question

In the figure, O is the centre of a circle and angle $\angle OBA=60{}^\circ$ . Then $\angle ACB$ equals:

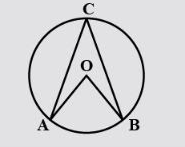
A.$60{}^\circ$
B.$75{}^\circ$
C.$120{}^\circ$
D.$30{}^\circ$

Answer 1

Hint:Start by using the property that angles opposite to equal sides are equal followed by the theorem that angle at the centre of the circle is twice the angle at the circumference.

Complete step-by-step answer:
Now let us start the above question by making some constructions according to our needs. .

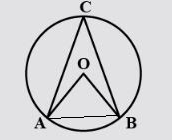
Now using the theorem that the angle at the circumference of a circle is half of the angle at the centre of the same circle, we can say:
$\angle ACB=\dfrac{1}{2}\angle AOB...........(i)$
Now applying the property that angles opposite to equal sides of a triangle are equal in $\Delta AOB$, in which AO=AB=radius, we get
$\angle BAO=60{}^\circ$
We also know that the sum of all the angles of a triangle is equal to $180{}^\circ$ .
$\therefore \angle AOB+\angle OBA+\angle OAB=180{}^\circ$
Now we will put the known values in the equation. On doing so, we get
$\angle AOB+60{}^\circ +60{}^\circ =180{}^\circ$
$\Rightarrow \angle AOB=60{}^\circ$
Now we will substitute the value of $\angle AOB$ in equation (i). On doing so, we get
$\angle ACB=\dfrac{1}{2}\times 60{}^\circ =30{}^\circ$
Therefore the answer to the above question is option (d) $30{}^\circ$ .

Note: Remember that the theorems related to cyclic quadrilateral are not valid for any regular quadrilateral. Also, it is prescribed to learn all the basic theorems related to circle as they are regularly used in the questions related to circles and cyclic quadrilaterals, as we did in the above question.