Solveeit Logo
Login

Question

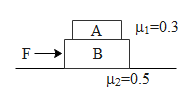
Question: In the figure, \({{m}_{A}}=3kg\) and \({{m}_{B}}=4kg\).For what minimum value of F, A starts slippin...

In the figure, mA=3kg{{m}_{A}}=3kg and mB=4kg{{m}_{B}}=4kg.For what minimum value of F, A starts slipping over B: (g=10ms−2)(g=10m{{s}^{-2}})

a) 50N
b) 59N
c) 36N
d) 45N

Explanation

Solution

In the above diagram we can see that there exists friction between the horizontal surface and between blocks A and B. It is to be noted that on application of force on B, block A will move back. But due to friction it will hold itself on the block B. The block A will slip on block B when the maximum acceleration due to the limiting friction of block A is given to block B. Hence using this condition we will accordingly find the maximum value of F.

Formula used:
NA=mAg and NB=(mA+mB)g{{N}_{A}}={{m}_{A}}g\text{ and }{{N}_{B}}=\left( {{m}_{A}}+{{m}_{B}} \right)g
F−μ2NB−μ1NA=mBaMAXF-{{\mu }_{2}}{{N}_{B}}-{{\mu }_{1}}{{N}_{A}}={{m}_{B}}{{a}_{MAX}}

Complete step by step answer:
In the above diagram we can see that both the blocks along there are subjected to frictional force. The frictional force is defined as the product of normal reaction times the coefficient of friction. Force of friction on block A is given by,
FA=μ1NA FA=μ1mAg \begin{aligned} & {{F}_{A}}={{\mu }_{1}}{{N}_{A}} \\\ & {{F}_{A}}={{\mu }_{1}}{{m}_{A}}g \\\ \end{aligned}
Similarly the force of friction by the bottom surface on block B is given by,
FB=μ2NB FB=μ2(mA+mA)g \begin{aligned} & {{F}_{B}}={{\mu }_{2}}{{N}_{B}} \\\ & {{F}_{B}}={{\mu }_{2}}\left( {{m}_{A}}+{{m}_{A}} \right)g \\\ \end{aligned}
The block A will move on B as long as the acceleration of the block does not cross the maximum value of acceleration due to the limiting force of friction i.e. (FA)({{F}_{A}}). Hence the maximum acceleration is given by,
FA=mAaMAX ⇒μ1mAg=mAaMAX ⇒μ1g=aMAX ⇒aMAX=0.3×10=3ms−2 \begin{aligned} & {{F}_{A}}={{m}_{A}}{{a}_{MAX}} \\\ & \Rightarrow {{\mu }_{1}}{{m}_{A}}g={{m}_{A}}{{a}_{MAX}} \\\ & \Rightarrow {{\mu }_{1}}g={{a}_{MAX}} \\\ & \Rightarrow {{a}_{MAX}}=0.3\times 10=3m{{s}^{-2}} \\\ \end{aligned}
If block B starts moving with this acceleration then the blocks will hardly move together. But if the acceleration of the block B is slightly greater than this the block A will slip over B. The force of friction acts on the top of block B as well as its bottom. Hence taking the maximum acceleration of the block B such that the block A does not slip over it the force on block B can be written as,
F−FB−FA=mBaMAX ⇒F−μ2NB−μ1NA=mBaMAX ⇒F=μ2NB+μ1NA+mBaMAX ⇒F=μ2(mA+mB)g+μ1mAg+mBaMAX ⇒F=0.5(3+4)10+0.3×3×10+5×3 ⇒F=35+9+15 ⇒F=59N \begin{aligned} & F-{{F}_{B}}-{{F}_{A}}={{m}_{B}}{{a}_{MAX}} \\\ & \Rightarrow F-{{\mu }_{2}}{{N}_{B}}-{{\mu }_{1}}{{N}_{A}}={{m}_{B}}{{a}_{MAX}} \\\ & \Rightarrow F={{\mu }_{2}}{{N}_{B}}+{{\mu }_{1}}{{N}_{A}}+{{m}_{B}}{{a}_{MAX}} \\\ & \Rightarrow F={{\mu }_{2}}\left( {{m}_{A}}+{{m}_{B}} \right)g+{{\mu }_{1}}{{m}_{A}}g+{{m}_{B}}{{a}_{MAX}} \\\ & \Rightarrow F=0.5\left( 3+4 \right)10+0.3\times 3\times 10+5\times 3 \\\ & \Rightarrow F=35+9+15 \\\ & \Rightarrow F=59N \\\ \end{aligned}

So, the correct answer is “Option B”.

Note:
It is to be noted that all the physical units have to be in SI units. Otherwise the answer obtained will not be in standard units. To solve the above question it is always necessary to draw the free body diagram for simplicity.