Question

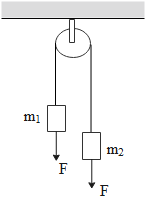
In the figure, ${{m}_{1}}=5kg$, ${{m}_{2}}=2kg$ and $F=1N$. Find the acceleration of either block. Describe the motion of $m_1$ if the string breaks but F continues to act.

Answer 1

When an object is attached to a point with a string a tension force is connected to the string in the upward direction. When an object is hanging on a massless string a gravitational pull also acts on the body. The study of these forces can be done with the help of FBD (free body diagram) and their forces are used to balance the other forces to maintain the inertia of the object (mass).
As per the given data,
The mass of one block is ${{m}_{1}}=5kg$
The mass of another block is ${{m}_{2}}=2kg$
The force acting downward other than the gravitational pull is $F=1N$

Complete answer:
When we draw a free body diagram for both the blocks attached to the string.
The FBD of the block of mass ${{m}_{1}}$ can be given as in the diagram here,

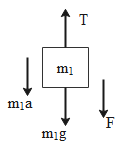
The force balancing equation of mass ${{m}_{1}}$ can be written as,
$\begin{aligned} & T={{m}_{1}}g-{{m}_{1}}a+F \\\ & \Rightarrow {{m}_{1}}a={{m}_{1}}g+F-T\quad ...\left( 1 \right) \\\ \end{aligned}$
The FBD of the block of mass ${{m}_{2}}$ can be given as in the diagram here,

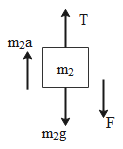
The force balancing equation of mass ${{m}_{2}}$ can be written as,
$\begin{aligned} & T-{{m}_{2}}a=mg+F \\\ & \Rightarrow {{m}_{2}}a=T-{{m}_{2}}g-F\quad ....\left( 2 \right) \\\ \end{aligned}$
Adding equation (1) and (2):
$a=\dfrac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
By putting the values of ${{m}_{1}}$ and ${{m}_{2}}$
$\begin{aligned} & a=10\left( \dfrac{3}{7} \right) \\\ & \therefore a=4.2m{{s}^{-2}} \\\ \end{aligned}$
Thus, the acceleration acting on the blocks will be $4.2m{{s}^{-2}}$
When the string breaks the block will move towards the direction of applied force $F$ (Towards the ground). Then the forces acting on the block will be equated as,
${{m}_{1}}a=F+{{m}_{1}}g$
By putting the value of ${{m}_{1}}$ the acceleration acting on the block will be given as,
$\begin{aligned} & \Rightarrow 5a=1+5g \\\ & \therefore a=g+0.2m{{s}^{-2}} \\\ \end{aligned}$
Thus, the acceleration of mass ${{m}_{2}}$and ${{m}_{1}}$ will be the same when they are attached to the string and the value of acceleration is $4.2m{{s}^{-2}}$. When the string breaks the acceleration of the block ${{m}_{1}}$ will be $g+0.2m{{s}^{-2}}$. And these are the required answers to the question.

Note:
When an object attached to the string is facing a certain force and breaks after a certain period of time its acceleration will increase to balance the force. This increase in energy is due to the conversion of the potential energy that the object holds at a certain height to the kinetic energy. This conversion gives proof for the law of conservation of energy.