Question
Question: In the figure \(\left( A \right)\) and \(\left( B \right)\) \(AC,\,DG,\,\) and \(GF\) are fixed incl...
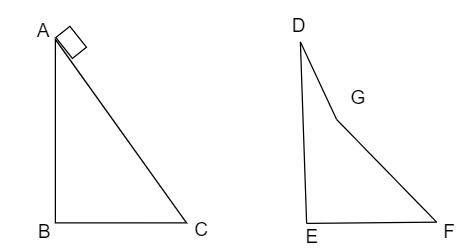
In the figure (A) and (B) AC,DG, and GF are fixed inclined planes, BC=EF=x and AB=DE=y. A small block of mass M is released from the point A . It slides down AC and reaches C with a speed vc . The same block is released from rest from the point D . It slides down DGF and reaches the point F with speed vF . The coefficient of kinetic frictions between the block and both the surfaces AC and DGF are μ . Calculate vc and vF .
Solution
Hint Analyse the diagram given in the question, and derive the equation of the motion of the block from that. Use the potential energy and the kinetic energy in it. The simplification of the above equation provides the value of the velocity of the block.
Useful formula
(1) The formula of the potential energy is given by
P=mgh
Where P is the potential energy, m is the mass of the block, g is the acceleration due to gravity and h is the height.
(2) The formula of the kinetic energy is given by
K=21mv2
K is the kinetic energy, v is the velocity of motion.
Complete step by step solution
It is given that the
AC,DG, and GF are fixed inclined planes
BC=EF=x
AB=DE=y
The speed at which the AC reaches C is vc .
The speed at which the block slides down AC and reaches C is vc
The coefficient of the kinetic friction is considered as μ
It is known that the potential energy of the block is converted into the kinetic energy while moving.
P−K=f2s1+f2s2
Substituting the formula in it,
mgy−21mvF2=μmgcosβS1−μmgcosαS2
By simplifying the above equation, we get
vF=2g(y−μx)
Note The friction affects the motion of the body when it rolls or slides down the surface. This is because the surface with the diffraction is rough and this reduces the velocity . This sliding motion is due to the acceleration due to gravity and not due to the external force applied on it.
