Question
Question: In the figure, initially the system is at rest. Find the minimum value of F for which sliding starts...
In the figure, initially the system is at rest. Find the minimum value of F for which sliding starts between the two blocks. Given, mA=10kg and mB=20kg.
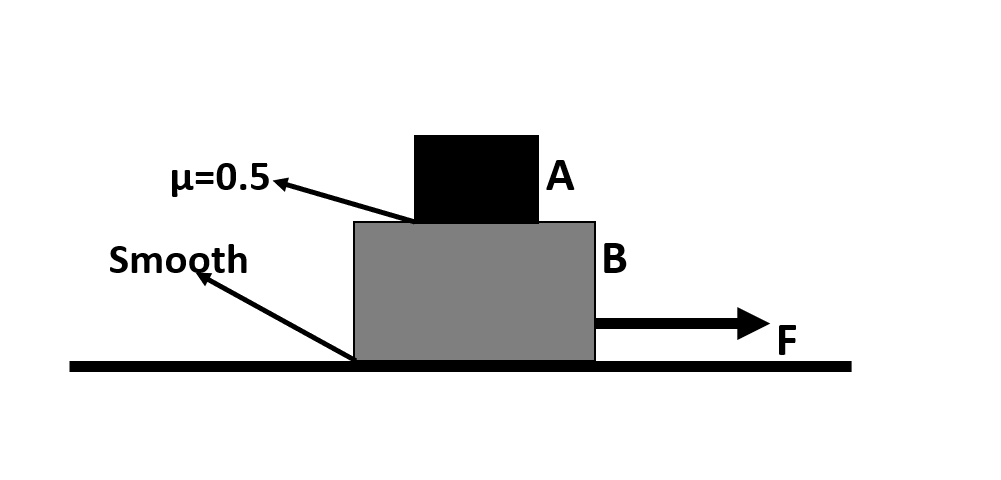
Solution
For sliding to start between the two blocks, the net pseudo force on the upper block in left direction due to the force F, should be more than the net frictional force between the two blocks which is acting on A in the right direction. We will work on this condition to find out the minimum value of F for which sliding starts between the two blocks.
Complete answer:
Let the combined acceleration of block A and block B just before the sliding starts be given by ‘a’.
Then, as the surface between B and the ground is frictionless, we can write as:
⇒F=(20+10)a∴F=30a
Now, the pseudo force acting in the left direction on block A can be calculated as the product of its mass and acceleration. Mathematically, that is:
⇒Fseudo=10×30F∴Fseudo=3F
And, the maximum frictional force acting on the block in the right direction is equal to:
⇒f=μN⇒f=0.5×(10×10)⇒f=50N
The sliding between the blocks will occur when the net pseudo force overtakes the net frictional force. Thus, it will start at the limiting condition. Mathematically, that is:
⇒Fseudo=f
Putting the values of these known terms, we get:
⇒3F=50N∴F=150N
Hence, the minimum value of applied force F for which sliding starts between the two blocks is equal to 150N.
Note:
We should be always careful while writing the direction of friction. And the best way to determine the direction of friction is by analyzing the relative motion between any two objects. Friction always opposes the relative motion between two objects. This concept has no exceptions and is fool proof at every situation. So, one should always remember it.
