Question
Question: In the figure, in a circuit, there are two motors, one is the Arm motor of \[12\] watts and the seco...
In the figure, in a circuit, there are two motors, one is the Arm motor of 12 watts and the second one is the Wheel motor of 18 watts and one 6 volts battery. Motors are in parallel connection. There are three points 1, 2 and 3 shown in the figure. Which of the following lists these three points in order from lowest to highest current?
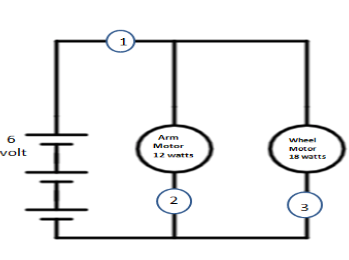
(A) 1,2,3
(B) 1,3,2
(C) 2,1,3
(D) 2,3,1
(E) 3,2,1
Solution
The current is passing through points 1, 2 and 3. There are acting two resistances along with two motors i.e. points 2 and 3.
Also, the equivalent resistance of these two resistances is acting in point 1.
We can calculate the value of the resistances by the given voltage and pressures of the motors.
We can calculate the value of the current of each point using Ohm’s law.
Hence we found the increasing order (lowest to highest) of flowing current along with the given points.
Formula used:
R1,R2,R3 are the resistances of the points 1, 2 and 3 respectively.
And, R1 is the equivalent resistance of R2and R3.
Since R2∣∣R3
∴R1=R2+R3R2R3,
R2=PArm−motorV2 and R3=PWheel−motorV2
V is the voltage of the battery.
I1,I2,I3 are the Current of the points1, 2 and 3 respectively.
According to Ohm’s law, I1=R1V,
I2=R2V
I3=R3V
Complete step by step answer:
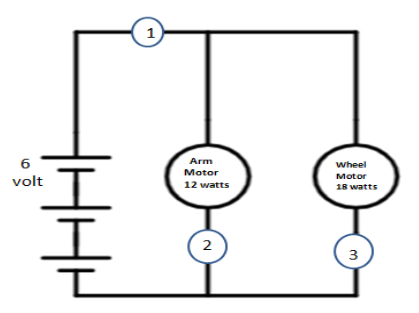
In the question stated as the current is passing through points 1, 2 and 3.
There are acting two resistances along with two motors i.e. points 2 and 3.
Also, the equivalent resistance of these two resistances is acting in point 1.
HereR1,R2,R3 are the resistances of the points 1, 2 and 3 respectively.
Also, R1 is the equivalent resistance of R2 and R3.
Here I1,I2,I3 are the Current of the points 1, 2 and 3 respectively.
Also, I1 is the total current of the circuit.
I1=R1V
I2=R2Vand I3=R3V
Now, V is the voltage of the battery which is given 6 Volt.
Since the two motors are in parallel connection the voltage across them is the same as the voltage of the battery i.e. 6Volt.
The power of the Arm motor is PArm−motor=12watt.
So, we can write it as
R2=PArm−motorV2
Here V=6 and we get,
⇒R2=1262=3Ω
And, The power of the Wheel motor is PWheel−motor=18watt.
R3=PWheel−motorV2
Putting the values and we get,
⇒R3=1862=2Ω
Since,R2∣∣R3
∴R1=R2+R3R2R3
Putting the finding values in R1 and we get,
∴R1=3+23×2=56Ω
∴ The total current of the circuit I1=R1V=566=5A. (Current flowing through point 1 )
Also, the current flowing through the two motors are,
I2=R2V=36=2A (Current flowing through point 2 )
I3=R3V=26=3A (Current flowing through point 3 )
So, the order of the given three points (1,2, and 3) according to the value of the lowest to the highest current flowing through them is 2,3,1.
Hence the right option is in option (D).
Note: It has to be noted that we take the voltage drop across the two resistances along the two motors is 6 volt which is the voltage of the battery Since the two motors are in parallel connection.
Similarly, the resistances along them are also in parallel connection as they are acting along with the two motors.
