Question

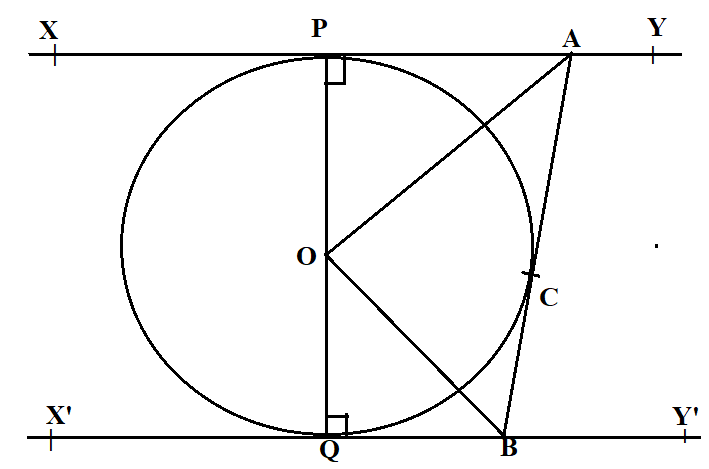
In the figure given below, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' at B. prove that ∠AOB = 90°

Answer 1

Hint- Proceed the solution of this question by joining Center to point C. Here you have to prove ∠ AOB = ${90^0}$, so if you prove sum of other two angle of Δ AOB equal to ${90^0}$ then automatically ∠ AOB will be equal to ${90^0}$because we know that sum of all angles of triangle equal to ${180^0}$.

Complete step by step answer:

In this question it is given that
XY is a tangent at point P and X’Y’ is a tangent at point Q
And XY || X’Y’
AB is a tangent at point C
We have to prove ∠ AOB = ${90^0}$
Proof-
Here we have a need of slight construction.
Join OC

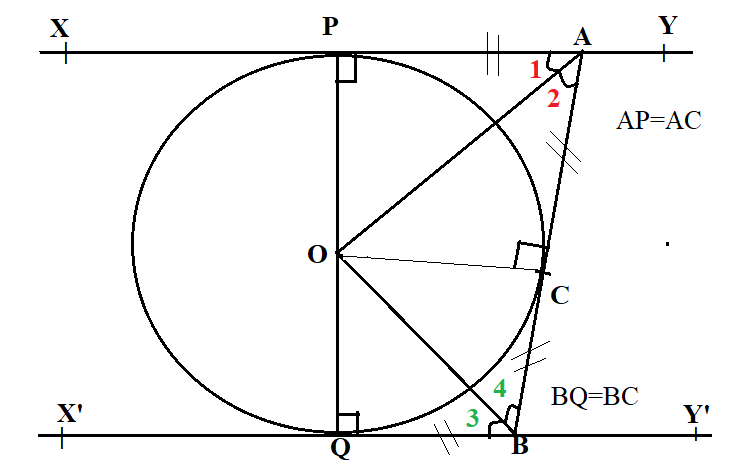
Now look at the triangles OPA and OCA
In Δ OPA and Δ OCA
⇒OP = OC (because OP and OC are radii of the same circle whose centre is o) ……. (1)
⇒PA = CA (length of two tangents from same point to the circle will be equal) …… (2)
⇒AO = AO (AO is a Common side for both triangle OPA and OCA) ………. (3)
We know that
SSS Congruence Rule
In two triangles, if the three sides of one triangle is equal to the three sides (SSS) of the other triangle, then the two triangles will be congruent.
On the behalf of (1), (2) and (3)
Triangles OPA and OCA will be congruent.
Δ OPA ≅ Δ OCA (By SSS congruence rule)
CPCT Rule
It stands for Corresponding parts of Congruent triangles. This theorem states that if two triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also equal to each other.

Hence, ∠ 1 = ∠ 2 (by CPCT rule)

Now look at the triangles OQB and OCB
In Δ OQB and Δ OCB
⇒OQ = OC (because OQ and OC are radii of the same circle whose centre is o) ……. (4)
⇒QB = BC (length of two tangents from same point to the circle will be equal) …… (5)
⇒BO = BO (AO is a Common side for both triangle OQB and OCB) ………. (6)
On the behalf of (4), (5) and (6)
Triangles OQB and OCB will be congruent.
Δ OQB ≅ Δ OCB (By SSS congruence rule)
Hence, ∠ 3 = ∠ 4 (by CPCT rule)
We know that,
If two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary or their sum will be ${180^0}$
So in the above figure
XY and X'Y' are two parallel lines cut by transversal AB
Hence, ∠ PAB + ∠ QBA = 180° ……. (7)
⇒∠ PAB = ∠1+∠2 ($\because$ = ∠1=∠2 )
$\therefore$ ∠ PAB = 2∠2
⇒∠ QBC = ∠3+∠4 ($\because$ = ∠3=∠4 )
$\therefore$ ∠QBC = 2∠4
On Putting ∠ PAB & ∠ QBA in equation (7)
⇒ 2∠2 + 2∠4 = 180°
On dividing by 2 on both side
⇒ ∠2 + ∠4 = 90° ………. (8)
Now see in triangle AOB
∠AOB+∠ABO+∠BAO=180° (sum of all interior angles of triangles always 180° know as Angle sum property)
⇒∠AOB +∠2 + ∠4 = 180°
On putting ∠2 + ∠4 = 90° from equation (8)
⇒∠AOB +90° = 180°
⇒∠AOB = 180° - 90°
⇒∠AOB = 90°
Hence proved.

Note- In this particular question where we have to prove something then, we have to start with proper construction, sometimes we can visualise it easily like in this question, by joining O to C, we got 4 triangles, and further by applying SSS congruence and CPCT rule of triangle, we establish a relation between angles of Δ AOB. Once we got the relation between angles of Δ AOB, so on substituting values of known angles and can prove the desired one.