Question
Question: In the figure given below, with what acceleration does the block of mass \(m\) will move? (Pulley an...
In the figure given below, with what acceleration does the block of mass m will move? (Pulley and strings are massless and frictionless).
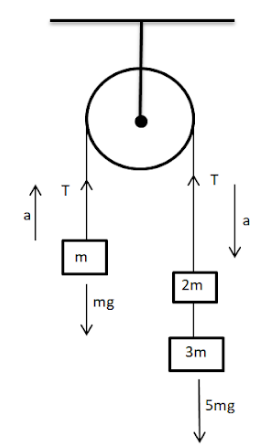
Solution
All that is required is the balancing of the forces. The net external force is equal to the sum of the forces acting on the object. Also keep in mind the tension force which comes along whenever strings/ropes are into play.
Complete step by step answer:
According to Newton’s second law of motion, F=ma where F is the net external force, m is the mass of the body and a is the acceleration with which the body moves. According to Newton’s third law of motion,to every action there is an equal and opposite reaction force.We know that all physical objects that are in contact can exert forces on each other.Tension is the force exerted by a rope,string,chain etc.Tension is a pulling force transmitted along the axis.
For an object with mass m, the net external force acting on it is the sum of all the forces acting on the object. And according to the second law, net external force is equal to ma.
Let T be the tension in the string going over the pulley. Therefore ma=T+(−mg).......[mg is in the opposite direction to that of the external force,hence a negative sign.]
T−mg=ma
⇒T=ma+mg--equation 1
Let us consider the right hand masses as a single unit of mass 5m (3m+2m). For an object with mass 5m, the net external force acting on it is the sum of all the forces acting on the object. Net external force is equal to 5ma. (According to second law)
Therefore 5ma=5mg+(-T )......[ T is in the opposite direction to that of the external force.]
5mg−T=5ma
⇒5mg−5ma=T--equation 2
Substituting value of T from equation 1 in equation 2, we get
5mg−5ma=ma+mg
⇒5mg−mg=ma+5ma
⇒4mg=6ma
⇒a=64g
∴a=32g
Hence the acceleration of the block of mass m is 32g.
Note: Two or more physical objects that are in contact, exert forces on each other.Based on the objects in contact we give these contact forces different names. If one of these objects in contact happens to be a string, rope, cable or spring, we call the force as tension.
