Question
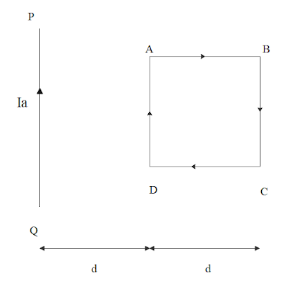
Question: In the figure given below, wire PQ is fixed while the square loop ABCD is free to move under the inf...
In the figure given below, wire PQ is fixed while the square loop ABCD is free to move under the influence of currents flowing in them. State with reason, in which direction does the loop begin to move or rotate?
Solution
To find out the direction of the movement of the loop, we need to understand the forces that are involved in the loop. We need to compare the forces on all the sides of the loop to trace out the path that it takes to move or rotate.
Formula used: In this question, we will be using the following formula,
⇒F=B.I.d
where F is the force,
B is the magnetic field,
I is the current in the wire,
and d is the distance
⇒τ=M×B
where τ is the torque
M is the magnetic moment and
B is the magnetic field.
Complete step by step answer
According to the figure given in the question, let us consider a square loop of side ABCD with current flowing through it and is denoted by I . And the current flowing in the wire PQ is Ia .
We can see that the sides AB and CD are at equal distance from the current carrying wire PQ. Thus, the force on the sides AB and CD are equal and opposite to each other and so they cancel out each other.
Now, we have to consider the sides AD and BC.
Force on the side AD can be calculated using the formula,
⇒FAD=B.I.d
The magnetic field at a distance d due to the wire PQ is B=4πμ0×dIa
⇒FAD=4πμ0×dIa×2×I×d
When we simplify this, we get,
⇒FAD=2πμ0.I.Ia
This force is acting on the side AD towards the wire.
The side BC is at a distance 2d from the wire PQ. So similarly then, the force on the side BC will be,
⇒FBC=4πμ0×2dIa×2×I×d
When we simplify, we get,
⇒FBC=4πμ0.I.Ia
This force is acting on the side BC away from the wire.
Thus, we can see that the force on the side AD is more than the force on the side BC.
Thus, the net force is towards the wire.
Let us find out whether the loop rotates or not using the torque formula. It comes as,
⇒τ=M×B
But, this is zero, as M and B are both directed towards the page. So the angle between them is zero.
Thus, we can conclude that the loop is not rotating. It moves towards the wire because of the net force of attraction towards the wire PQ.
Note
When a current carrying loop is placed in a magnetic field it experiences a force that is acting on this. This is the principle that is used in motors. There the magnetic field is kept perpendicular to the loop and hence it experiences a torque due to which it rotates.
