Question

In the figure given below (not to scale), $AM:MC = 3:4$, $BP:PM = 3:2$ and $BN = 12{\text{ cm}}$. Then AN is

Answer 1

First, we will construct $MR||CN$ and $MR||PN$. Then we will take triangle $\Delta BMR$ and use the basic proportionality theorem, $\dfrac{{BN}}{{NR}} = \dfrac{{BP}}{{PM}}$. Then we will take triangle $\Delta ANC$and use the basic proportionality theorem in $\Delta ANC$. Then we will add the value of AR and RN to find the value of AN.

Complete step by step answer:

We are given that $AM:MC = 3:4$, $BP:PM = 3:2$ and $BN = 12{\text{ cm}}$.
Now, we will construct $MR||CN$ and $MR||PN$.

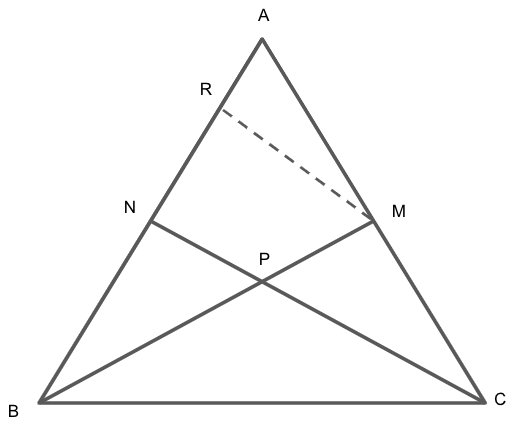
In triangle $\Delta BMR$, we have
We know that the basic proportionality theorem, which states that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.$\Rightarrow \dfrac{{12}}{{NR}} = \dfrac{3}{2}$
Using the above basic proportionality theorem in $\Delta BMR$, we get
$\dfrac{{BN}}{{NR}} = \dfrac{{BP}}{{PM}}$
Substituting the value of $BN$ and $\dfrac{{BP}}{{PM}}$ in the above equation, we get
Cross-multiplying the above equation, we get
$\Rightarrow 24 = 3NR$
Dividing the above equation by 3 on both sides, we get

$$\Rightarrow \dfrac{{24}}{3} = \dfrac{{3NR}}{3} \\\ \Rightarrow NR = 8{\text{ cm}} \\\$$

In triangle $\Delta ANC$, we have
Using the above basic proportionality theorem in $\Delta ANC$, we get
$\dfrac{{AR}}{{RN}} = \dfrac{{AM}}{{MC}}$
Substituting the value of $RN$ and $\dfrac{{AM}}{{MC}}$ in the above equation, we get
$\Rightarrow \dfrac{{AR}}{8} = \dfrac{3}{4}$
Cross-multiplying the above equation, we get
$\Rightarrow 4AR = 24$
Dividing the above equation by 4 on both sides, we get

$$\Rightarrow \dfrac{{3NR}}{3} = \dfrac{{24}}{3} \\\ \Rightarrow AR = 6{\text{ cm}} \\\$$

Adding the value of AR and RN to find the value of AN, we get

$$\Rightarrow AN = 6 + 8 \\\ \Rightarrow AN = 14{\text{ cm}} \\\$$

Thus, the value of AN is 14 cm.

Note: In solving these types of questions, first draw the pictorial representation of the given problem for better understanding. You need to know the properties of triangles and their midpoint. Then we will use the properties accordingly. The basic proportionality theorem, which states that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.