Question
Question: In the figure given below, \(CDE\) is straight line and \(A,B,C\) and \(D\) are points on a circle. ...
In the figure given below, CDE is straight line and A,B,C and D are points on a circle. ∠BCD=44∘, find the value of x.
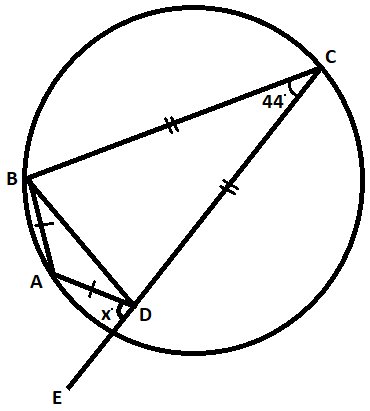
Solution
To solve the above problem we have to know a few properties of a quadrilateral inscribed inside a circle. There are a few properties such as the sum of the opposite angles of a quadrilateral in a circle is 180∘, as long as the quadrilateral does not cross itself out of the circle. Here a four-sided polygon is inscribed in a circle.
Complete step by step answer:
Given that ∠ADE=x∘
The opposite angles in a quadrilateral in a circle should be equal to 180∘, as long as the quadrilateral does not cross the circle.
∴∠BAD+∠BCD=180∘
As given that ∠BCD=44∘, substituting this in the above expression:
⇒∠BAD+44∘=180∘
⇒∠BAD=180∘−44∘
∴∠BAD=136∘
Now consider the triangle BCD, given that two sides are equal in this triangle, as given below:
⇒BC=CD
Hence the angles opposite to these sides will also be equal, which is given below:
⇒∠CBD=∠CDB
We know that the sum of the angles in a triangle should be equal to 180∘, as given below:
⇒∠CBD+∠BCD+∠CDB=180∘
⇒∠CBD+44∘+∠CDB=180∘
⇒2∠CDB=180∘−44∘
⇒2∠CDB=136∘
∴∠CDB=68∘
Hence ∠CBD=68∘
Now consider the triangle ABD, given that two sides are equal in this triangle, as given below:
⇒AB=AD
Hence the angles opposite to these sides will also be equal, which is given below:
⇒∠ABD=∠ADB
We know that the sum of the angles in a triangle should be equal to 180∘, as given below:
⇒∠ABD+∠BAD+∠ADB=180∘
We found that ∠BAD=136∘, substituting this in the above expression, as shown below:
⇒136∘+2∠ADB=180∘
⇒2∠ADB=180∘−136∘
⇒2∠ADB=44∘
⇒∠ADB=22∘
Hence ∠ABD=22∘
Now we know that a straight angle forms an angle of 180∘, which is as given below:
Consider the straight line at the point D, which is given below:
⇒∠CDB+∠ADB+∠ADE=180∘
⇒68∘+22∘+∠ADE=180∘
⇒∠ADE=180∘−90∘
⇒∠ADE=90∘
∴x=90∘
The value of x is 90∘.
Note: While solving such kinds of polygons inscribed inside a circle problems, one thing which is most important to remember is that the sum of the opposite angles of a quadrilateral which is in a circle is equal to 180∘. Also it is crucial to note that the sum of the angles in any quadrilateral is equal to 360∘.
