Question

In the figure given below: $AB=BC=CD=DE=EF=FG=GA$ , then find $\angle DAE$ (approximately).

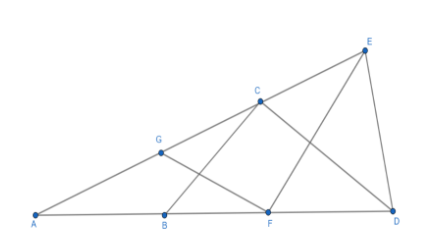
(a) ${{24}^{0}}$
(b) ${{25}^{0}}$
(c) ${{26}^{0}}$
(d) None of the above

Answer 1

To solve this question easily first we will understand some important properties related to triangles, especially isosceles triangles and exterior angle theorem to find the correct answer.

Complete step-by-step answer :
Given:

In the above figure: $AB=BC=CD=DE=EF=FG=GA$ .
Let, $\angle DAE=\theta$ .
Now, we will see 3 important properties related to triangles one by one which will be used to solve this problem.
First property:
Sum of interior angles of a triangle is always ${{180}^{0}}$ . It is a very basic property but very useful and important.
Second property:
It is also known as “Exterior Angle Theorem”. It states that if a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior angles. As shown in the figure below:

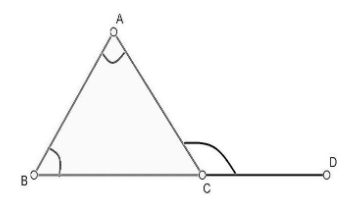
In the above figure, $\Delta ABC$ is shown in which side $BC$ is extended to $D$ . Then, from exterior angle theorem, we can write, $\angle DCA=\angle ABC+\angle CAB$ .
Third property:
Angles opposite to equal sides of an isosceles triangle are equal. This can be understood with the help of the figure below:

In the above figure, $\Delta ABC$ is shown in which $AB=AC$ . Then, $\angle ABC=\angle ACB$ .
Now, we will use the above three properties collectively to solve the given problem.

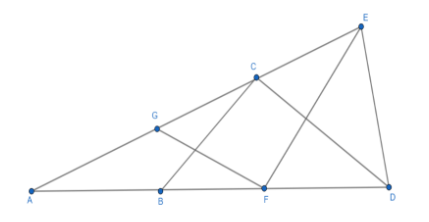
In the above figure:
In $\Delta ABC$ , it is given that $AB=BC$ . Then, from the third property of the isosceles triangle we get,
$\angle BAC=\angle ACB............\left( 1 \right)$
In $\Delta AGF$ , it is given that $FG=GA$ . Then, from the third property of the isosceles triangle we get,
$\angle FAG=\angle AFG........\left( 2 \right)$
If we look at the given figure then we can write that, $\angle DAE=\angle BAC=\angle FAG=\theta$ . Then,
From (1) and (2) we get, $\angle DAE=\angle BAC=\angle ACB=\angle FAG=\angle AFG=\theta$ .
Now, in $\Delta BCD$ , it is given that $BC=CD$ . Then, from the second property of the isosceles triangle we get, $\angle DBC=\angle CDB$ and let, $\angle DBC=\angle CDB=\beta$ .
Now, if we look in the given figure and consider $\Delta ABC$ then, we will find that the side $AB$ is extended to $D$ . So, we can apply the second property of exterior angle theorem. Then,
$\begin{aligned} & \angle DBC=\angle BAC+\angle ACB \\\ & \Rightarrow \beta =\theta +\theta \\\ & \Rightarrow \beta =2\theta ........\left( 3 \right) \\\ \end{aligned}$
Now, in the given figure consider $\Delta GFE$ , it is given that $EF=FG$ . Then, from the third property of the isosceles triangle we get, $\angle FGE=\angle FEG$ and let, $\angle FGE=\angle FEG=\delta$ .
Now, if we look in the given figure and consider $\Delta AGF$ then, we will find that the side $AG$ is extended to $E$ . So, we can apply the second property of the exterior angle theorem. Then,
$\begin{aligned} & \angle FGE=\angle FAG+\angle AFG \\\ & \Rightarrow \delta =\theta +\theta \\\ & \Rightarrow \delta =2\theta ........\left( 4 \right) \\\ \end{aligned}$
Now, in the given figure consider $\Delta DEF$ , it is given that $DE=EF$ . Then, from the third property of the isosceles triangle we get, $\angle DFE=\angle FDE$ and let, $\angle DEF=\angle FDE=\alpha$ .
Now, if we look in the given figure and consider $\Delta AEF$ then, we will find that the side $AF$ is extended to $D$ . So, we can apply the second property of the exterior angle theorem. Then,
$\angle DFE=\angle FAE+\angle AEF$
In the above equation we can substitute, $\angle FAE=\angle BAC=\theta$ and $\angle AEF=\angle FEG=\delta$. Then,
$\angle DFE=\theta +\delta$
Now, from (4) put $\delta =2\theta$ in the above equation. Then,
$\begin{aligned} & \angle DFE=\theta +2\theta \\\ & \Rightarrow \alpha =3\theta ...........\left( 4 \right) \\\ \end{aligned}$
Now, in the given figure consider $\Delta DCE$ , it is given that $CD=DE$ . Then, from the third property of the isosceles triangle we get, $\angle DCE=\angle DEC$ and let, $\angle DCE=\angle DEC=\gamma$ .
Now, if we look in the given figure and consider $\Delta ACD$ then, we will find that the side $AC$ is extended to $E$ . So, we can apply the second property of the exterior angle theorem. Then,
$\angle DCE=\angle DAC+\angle CDA$
In the above equation we can substitute, $\angle DAC=\angle BAC=\theta$ and $\angle CDA=\angle CDB=\beta$ . Then,
$\angle DCE=\theta +\beta$
Now, from (3) put $\beta =2\theta$ in the above equation. Then,
$\begin{aligned} & \angle DCE=\theta +2\theta \\\ & \Rightarrow \gamma =3\theta .............\left( 5 \right) \\\ \end{aligned}$
Now, in the given figure consider $\Delta DAE$ . Then in $\Delta DAE$ ,
$\angle DAE=\theta$ and $\angle ADE=\angle FDE=\alpha$ , $\angle DEA=\angle DEC=\gamma$ . Using the first property of the sum of interior angles of any triangle to be ${{180}^{0}}$ . We get,

& \angle DAE+\angle ADE+\angle DEA={{180}^{0}} \\\ & \Rightarrow \theta +\alpha +\gamma ={{180}^{0}} \\\ \end{aligned}$$ Now, using (4) and (5) substitute $\alpha =3\theta $ and $\gamma =3\theta $ in the above equation. Then, $$\begin{aligned} & \theta +\alpha +\gamma ={{180}^{0}} \\\ & \Rightarrow \theta +3\theta +3\theta ={{180}^{0}} \\\ & \Rightarrow 7\theta ={{180}^{0}} \\\ & \Rightarrow \theta =\dfrac{{{180}^{0}}}{7} \\\ & \Rightarrow \theta ={{\left( 25.71428 \right)}^{0}} \\\ & \Rightarrow \theta \approx {{26}^{0}} \\\ & \Rightarrow \angle DAE\approx {{26}^{0}} \\\ \end{aligned}$$ Thus, $\angle DAE={{26}^{0}}$ (approximately). Hence, (c) is the correct option. **Note** :Here, the student should apply the exterior angle theorem carefully stepwise and also use the property of the isosceles triangle correctly. Moreover, variables like $\theta ,\alpha ,\beta ,\gamma $ should be assigned carefully so that we will get the correct answer. And finally, match the most suitable option.