Question
Question: In the figure, find the area of the region in yellow color, enclosed between two concentric circles ...
In the figure, find the area of the region in yellow color, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC=40∘. Consider π=722 .
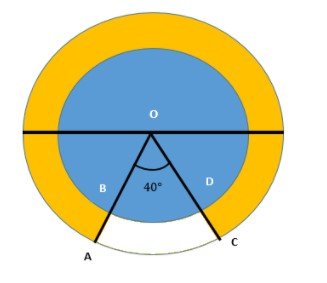
Solution
We will first find the area of the bigger circle and subtract the area of the smaller circle from it. Now, we will find the area of sector of bigger circle with ∠AOC=40∘ and subtract the area of sector of smaller circle from it and subtract the resultant from the resultant of difference of areas of complete circle, we will get the answer.
Complete step-by-step answer:
Let us first discuss the formulas we are going to use that is the area of a circle and area of sector.
Area of a circle is given by A=πr2, where r is the radius of the circle.
Area of a sector is given by A=360∘θ×πr2.
Now, let us say that r1=7 and r2=14.
So, let us find the area of the space which lies in a bigger circle but not in a smaller circle.
Area will be given by A1=πr22−πr12 which can be written as:-
A1=π(r22−r12)
Now, we will use the formula of a2−b2=(a−b)(a+b)
Hence, we have:- A1=π(r2−r1)(r2+r1)
Now, putting in all the values, we will get:-
A1=722(14−7)(14+7)
Simplifying it, we will get:-
A1=722×7×21=22×21=462cm2
Hence, A1=462cm2 ………(1)
Now, let us find the area which we need to subtract from (1) that is the difference of area of sectors of both the circles. We will get:-
A2=360∘θ×πr22−360∘θπr12
Rearranging the terms to get:-
A2=360∘θ×π(r22−r12)
Now, we will use the formula of a2−b2=(a−b)(a+b). So, we will get:-
A2=360∘θ×π(r2−r1)(r2+r1)
Now, putting in all the values, we will get:-
A2=360∘40∘×722(14−7)(14+7)
Simplifying it:
A2=91×722×7×21=3154cm2 ……….(2)
Now subtracting (2) from (1) will give us the required yellow region area.
Hence Area required = (462−3154)cm2 that is equivalent to (31232)cm2.
Note: The students must remember to put in the value of π as 722 as asked in question because using 3.14 may change the values required to us.Students should remember the definitions and formulas of area of circle and area of sector for solving these types of problems.
