Question
Question: In the figure D and E are points on the sides AB and AC respectively of a \(\vartriangle ABC\) such ...
In the figure D and E are points on the sides AB and AC respectively of a △ABC such that DE||BC and divides △ABC into two parts, equal in area, find ABBD.
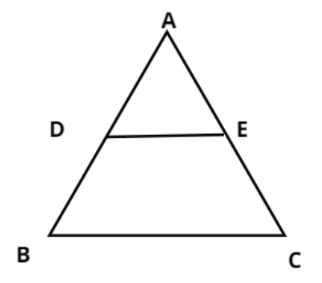
Solution
Hint: In this problem we have been with a triangle ABC such that the line segment DE inside this triangle is parallel to BC. So BCED forms a trapezium now and it is given that this DE divides this triangle into two equal areas. Thus use the respective formula for area of triangle and area of trapezium along with triangle congruence postulates to reach the answer.
Complete step-by-step answer:
It is given that the area of triangle ADE is equal to the area of trapezium BCED.
⇒Area(ΔADE)=Area(trapezium BCED)
Now add area of triangle ADE both sides we have
⇒Area(ΔADE)+Area(ΔADE)=Area(ΔADE)+Area(trapezium BCED)
In above equation R.H.S part is the total area of triangle ABC
⇒2Area(ΔADE)=Area(ΔABC)
⇒Area(ΔABC)Area(ΔADE)=21 …………………. (1)
Now in triangle ADE and in triangle ABC we have
∠ADE=∠B [\because DE||BC{\text{ & }}\angle ADE = \angle B (Corresponding angles)]
And, ∠A=∠A [common angle]
Therefore Area(ΔADE)≈Area(ΔABC) (similar triangles)
Therefore according the property of similar triangles
ABAD=ACAE=BCDE=Area(ΔABC)Area(ΔADE)
Now from equation (1) we have
ABAD=ACAE=BCDE=21=21
⇒AD=2AB……………………………. (2)
Now from figure we can say that
BD=AB−AD
Now from equation (2)
BD=AB−AD=AB−2AB
⇒ABBD=1−21.
So, this is the required ratio of BD to AB.
Thus, this is the required answer.
Note: Whenever we face such types of geometry questions the key point is to understand the diagrammatic representation of the data provided in the question. Having a good understanding of various triangle congruence postulates like ASA, AAA, SSS along with formulas of various sections like triangle and trapezium always helps in getting on the right track to reach the answer.
