Question
Question: \- In the figure, \({C_1} = {C_5} = 8.4\mu F\) and \({C_2} = {C_3} = {C_4} = 4.2\mu F\). The applied...
- In the figure, C1=C5=8.4μF and C2=C3=C4=4.2μF. The applied potential is Vab=220V. The equivalent capacitance of the network between points a and b is C. Calculate the value of 2C.
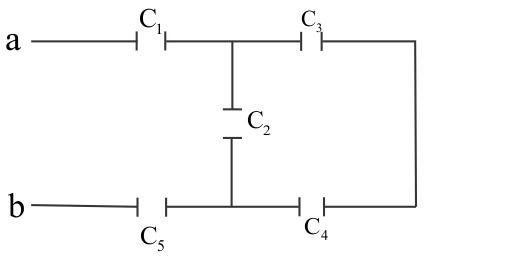
Solution
The equivalent capacitance in the circuit when capacitors are parallel to each other is calculated by –
Ceq=C1+C2+…Cn
And the equivalent capacitance in the circuit when capacitors are in series with each other is calculated by –
Ceq1=C11+C21+…+Cn1
where, n is the number capacitors.
Then, find the equivalent capacitance and multiply it by 2.
Complete step by step solution:
The circuit which has two or more electrical devices connected with it, then, there are many other ways by which we can connect them. They can either be series or parallel.
The circuit is said to be in series when two components in the circuit have a common node and the current which flows through all the components in the circuit is the same. In these types of circuits, there is only one path for the current. When the capacitors are connected in series, the equivalent capacitance is less than any one of the series capacitor’s individual response. The equivalent capacitance in series can be calculated by –
Ceq1=C11+C21+…+Cn1
The circuit is said to be parallel when there are multiple paths for the current to flow. In this type of circuit, all components have the same voltage across all ends. The equivalent capacitance in parallel can be calculated by –
Ceq=C1+C2+…Cn
Now, according to the question, it is given that –
C1=C5=8.4μF
C2=C3=C4=4.2μF
Vab=220V
Now, the equivalent capacitance between C3 and C4 are in series, so the equivalent capacitance is –
C341=C31+C41
Putting the values in above formula –
C341=4.21+4.21 C341=4.22 C34=2.1μF
So, the circuit can be drawn as –
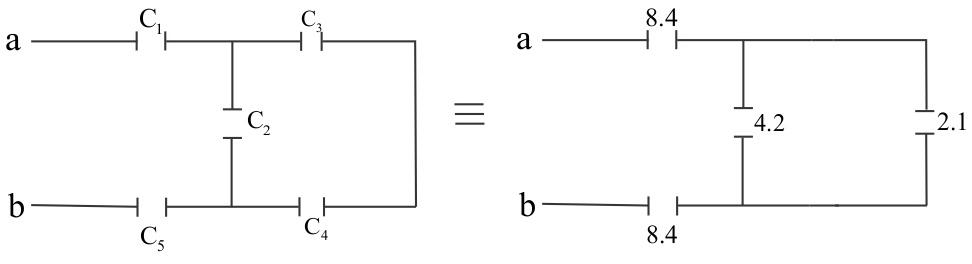
The capacitors 4.2 and 2.1 are parallel to each other so, the equivalent capacitance is –
C234=4.2+2.1 C234=6.3μF
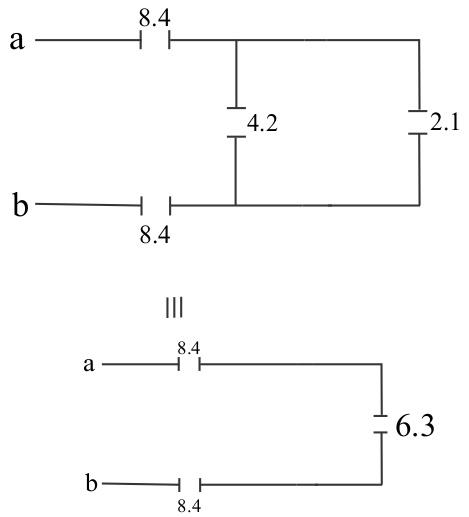
Now, the equivalent capacitance can be calculated by –
Ceq1=3.41+8.41+6.31
By further solving, we get –
Ceq=2.52μF
To calculate 2C we have to multiply the equivalent capacitance by 2, we get –
2Ceq=2×2.52=5.04μF
Hence, the value of 2C in the circuit is 5.04μF.
Note: When the capacitors are connected in series, the equivalent capacitance is less than any one of the series capacitor’s individual response. When the capacitors are in parallel with each other, then, the overall effect is that of a single equivalent capacitor having the sum total of the plate areas of the individual capacitors.
