Question

In the figure BC is the chord of the circle with centre O and A is a point on the minor arc BC. Then $\angle BAC+\angle OBC$ is equal to:

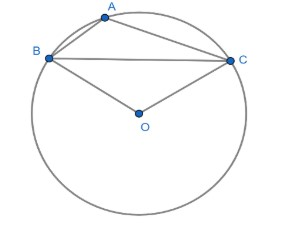
(a) 30
(b) 60
(c) 80
(d) 90

Answer 1

Hint:First we are going to use the property of the circle that the angle subtended by the chord at circumference is half the angle at the centre of the circle. Then we will write $\angle BAC$ in the form of $\angle BOC$ then we will look at triangle OBC and find the value of $\angle OBC$ and with the help of that we will find the value of$\angle BAC+\angle OBC$ .

Complete step-by-step answer:
Let’s first look at the figure,

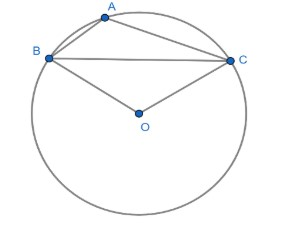
Now we will use the property of circle that the angle subtended by the chord at circumference is half the angle at centre of circle, to write $\angle BAC$ in the form of $\angle BOC$
So, we can write $\angle BAC$= $\dfrac{\angle BOC}{2}$
Now triangle OBC is isosceles because OC = OB = radius of the circle.
So, $\angle OCB=\angle OBC$
Now the sum of all the angles of the triangle is 180.
We will also use $\angle BAC$= $\dfrac{\angle BOC}{2}$,
$\begin{aligned} & \angle OBC+\angle OCB+\angle BOC=180 \\\ & 2\angle OBC+\angle BOC=180 \\\ & 2\left( \angle OBC+\angle BAC \right)=180 \\\ & \angle OBC+\angle BAC=90 \\\ \end{aligned}$
Hence we have found the value of $\angle BAC+\angle OBC= 90$.
So, the correct option is (d).

Note: We have used the property of a circle to find the relation between two angles. This property is very important while solving such type of questions. One should also use the fact that triangle OBC is isosceles, which is also very useful while solving this question.