Question

In the figure, $\angle PQR = 100^\circ$, when P, Q and R are points on a circle with centre O. Find$\angle OPR$.

Answer 1

To solve this kind of problem use the let us use the theorem of the circle that the angle made by arc at the centre is double of the angle made by the same arc at any point on the remaining part of the circle.

Complete step-by-step solution
Given,
In a given circle$\angle PQR = 100^\circ$, OP and OR are the radius of the circle.
Take point S, on the major arc of the circle and join with point P and R. Now PQRS is a cyclic quadrilateral inside the circle.

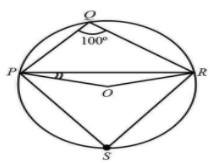
The sum of the opposite angle of the quadrilateral is$180^\circ$.
$\angle PQR + \angle PSR = 180^\circ$
Substitute the value of $\angle PQR = 100^\circ$ in above equation.
$\begin{array}{c} 100^\circ + \angle PSR = 180^\circ \\\ \angle PSR = 180^\circ - 100^\circ \\\ = 80^\circ \end{array}$
Now, PQR arc is subtended $\angle POR$ at the centre of circle, $\angle PSR$ at point S.
Apply the theorem of circle and determine the angle subtended by arc PQR at the centre of circle which is double of the angle subtended on point S.
$\begin{array}{c} \angle POR = 2\angle PSR\\\ = 2 \times 80^\circ \\\ = 160^\circ \end{array}$
From $\Delta PQR,$ OP and OR are equal because these are radius of circle, so the angle$\angle OPR\,$ and $\angle ORP$ will also be equal.
The sum of all angles of $\Delta OPR,$
$\angle POR + \angle OPR + \angle ORP = 180^\circ$
Substitute the values in the above equation and we know $\angle OPR\, = \,\angle ORP$.
$\begin{array}{c} 160^\circ + \angle OPR + \angle OPR = 180^\circ \\\ 2\angle OPR\, = 180^\circ - 160^\circ \\\ \angle OPR\, = \dfrac{{20^\circ }}{2}\\\ \angle OPR = 10^\circ \end{array}$
Therefore, the value of angle $\angle OPR = 10^\circ$.

Note: Use the concept of cyclic quadrilateral by taking point S on the periphery of the circle and making a cyclic quadrilateral PQRS inside a circle.To solve these type of problems have implement a small construction for the given figure to solve it easly.