Question
Question: In the Figure, an aluminum wire, of length \[{L_1} = 60.0cm\] cross-sectional area\[1.00 \times {10^...
In the Figure, an aluminum wire, of length L1=60.0cm cross-sectional area1.00×10−2cm2, and density2.60g/cm3, is joined to a steel wire, of density 7.80g/cm3 and the same cross-sectional area. The compound wire, loaded with a block of massm=10.0kg, is arranged so that the distance L2from the joint to the supporting pulley is86.6cm. Transverse waves are set up on the wire by an external source of variable frequency; a node is located at the pulley. Find the lowest frequency that generates a standing wave having the joint as one of the nodes.
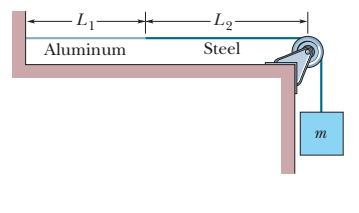
Solution
From the question, we absorbed that the length, cross-sectional area, and density are given for two sections. And also the mass of the loaded block is given. By using these data, first, we have to calculate the ratio of integers. After that, we will find the lowest frequency that generates a standing wave having the joint as one of the nodes.
Complete step by step answer:
The frequencies of the wave for both sections of the wire are the same. The wave speed and wavelength are different in different sections.
Suppose there are n1 loops in the aluminum section of the wire, then
L1=2n1λ1=2fn1v1 (∴λ1=fv1)
Where λ1is the wavelength and v1is the wave speed in that section.
Thus f=2L1n1v1
Similarly, for the steel section f=2L2n2v2
We know that the frequency is the same for the two sections 2L1n1v1=2L2n2v2
Now, the wave within the aluminum section is given byv1=μ1τ, where μ1is the linear mass density of the aluminum wire.
The mass of aluminum in the wire is given by m1=ρ1AL1where ρ1is the mass density for aluminum and Ais the cross-sectional area of the wire.
μ1=L1ρ1AL1=ρ1A and v1=ρ1Aτ
Similarly, the wave speed in the steel section v2=ρ2Aτ
We realized that the cross-sectional area and the tension are the same for the two sections. The equality of the frequency for two sections now leads toL1ρ1n1=L1ρ2n2. Where A has been canceled on both sides.
The ratio of the integers n1n2=L1ρ1L2ρ2=(0.600m)2.60×103kg/m3(0.866m)7.80×103kg/m3=2.50
The smallest integer that has this ratio is n1=2and n2=5
The frequency is f=2L1n1v1=(2L1n1)ρ1Aτ
The tension provided by the hanging block isτ=mg. Where m is the mass of the block.
Thus, f=2L1n1ρ1Amg=2(0.600m)2(2.60×103kg/m3)(1.00×10−6m2)(10kg)(9.80m/s2)=324Hz
Note: Steel is harder than aluminum, while rust could be a threat. Steel should be a solid material that’s less likely to warp, deform, or bend when subjected to weight, force, or heat. Nonetheless, steel's resilience comes at the price of being much stronger and denser than aluminum. Steel contains a density of 2.5 times that of aluminum.
