Question

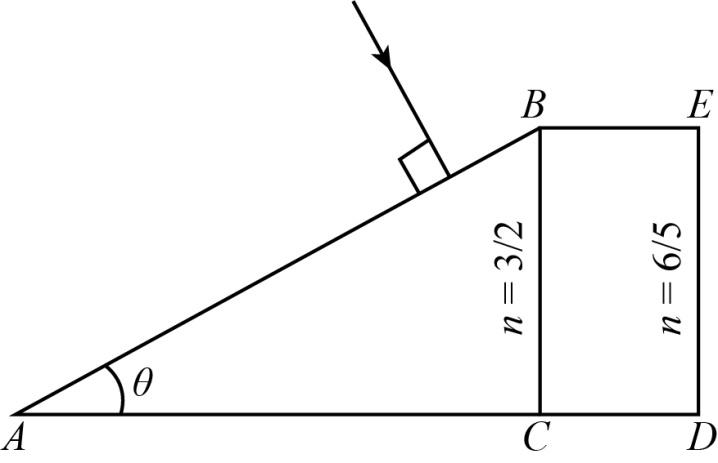
In the figure ABC is the cross section of a right angled prism and BCDE is the cross section of a glass slab. The value of θ so that light incident normally on the face AB does not cross the face BC is (given $sin-1{\rm{ }}\left( {\dfrac{3}{5}} \right){\rm{ }} = {\rm{ }}37^\circ$ )

A $\theta \le 37^\circ$
B $\theta > 37^\circ$
C $\theta \le 53^\circ$
D $\theta < 53^\circ$

Answer 1

In this question, we first consider the diagram when the ray enters the prism from the face AB. With the use of Snell’s law, the angle of incidence can be calculated. Then using angle sum property, theta can be calculated.

Complete step by step answer: Given: The refractive index of the prim is ${\mu _1} = \dfrac{3}{2}$, and The refractive index of the glass slab is ${\mu _2} = \dfrac{6}{5}$.

We see from the diagram that there is a prism and glass slab. The beam of light is incident on the prism normally on the face AB, in such a way that the light does not cross the BC.
To find the incident angle, we have to consider that the beam of light is entered in the prism normally with the angle $\theta$
Consider the diagram when the beam entered the glass slab.

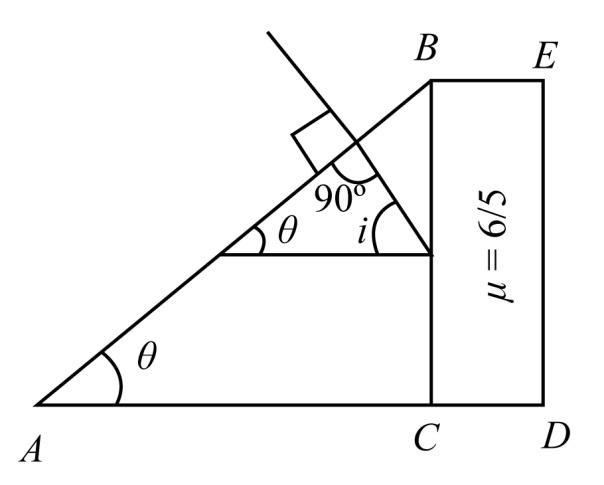
Now, to find the angle $\theta$we can use the Snell’s law,
${\mu _1}\sin i = {\mu _2}\sin r$
Here, $\sin i$ is the angle of incidence and ${\mathop{\rm sinr}\nolimits}$ is the angle of reflection.
Substitute the values in the above equation we get,
$\Rightarrow \dfrac{3}{2}\sin i = \dfrac{6}{5}\sin 90^\circ \\\ \Rightarrow \sin i = \dfrac{4}{5}\\\ \Rightarrow i = 53^\circ$
Therefore, the incident angle is $53^\circ$.
Now, to calculate the incident angle, we use the property of the triangle.
Therefore,
$\Rightarrow \theta + 90^\circ + i = 180^\circ \\\ \Rightarrow \theta + 90^\circ + 53^\circ = 180^\circ \\\ \Rightarrow \theta = 180^\circ - 143^\circ \\\ \Rightarrow \theta = 37^\circ$
Thus, the value of theta is $37^\circ$.
The incident angle is the critical angle, so $\theta$ must be less than $37^\circ$ so that light does not cross the face BC.
$\theta \le 37^\circ$

Thus, the correct option is (A).

Note: In this question, students must have the knowledge of the term reflection, refraction and critical angle. The critical angle is the angle of incidence that gives an angle of refraction of 90 degrees.