Question

In the figure, AB is a 300 cm long wire having resistance 10$\Omega {{m}^{-1}}$. Rheostat is set at 20 $\Omega$. The balancing point will be attained at –

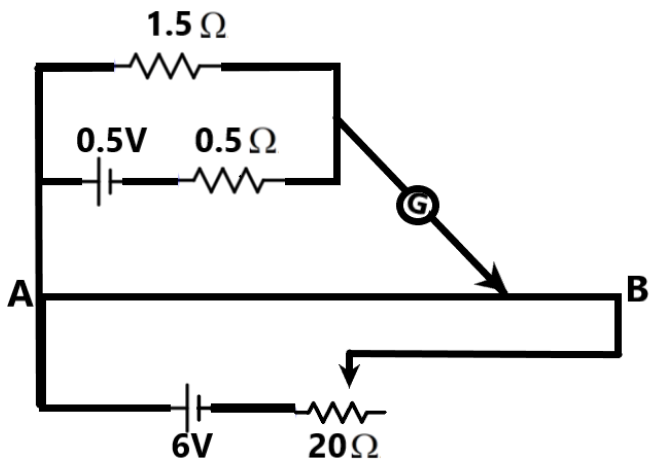
A) 1.0 m
B) 1.25 m
C) 1.5 m
D) Cannot be determined

Answer 1

We need to understand the relation between the resistance per unit length of a given material of wire, the resistance in the circuit and the emf in the external emf provided in a potentiometer setup to find the balancing point in the wire.

Complete answer:
We are given a potentiometer with an external cell connected to the terminal A of the setup. We know that the total current through the potentiometer is determined by the overall effect of the potential drops in the setup due to the operating voltage and the secondary voltage used in the potentiometer.
We know from Kirchhoff's voltage law that the sum of the voltages in a closed loop will always be zero. This is the governing principle of the potentiometer. When the galvanometer jockey is kept at the balancing point of the potentiometer, there will be no current through the wire AB.

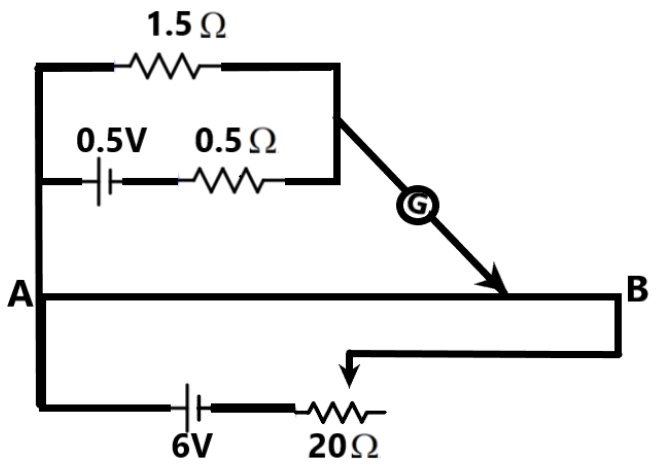
When there is no current through the external cell, the voltage drop across the wire AB is given as –

& \varepsilon ={{V}_{source}}\dfrac{{{R}_{AB}}}{{{R}_{AB}}+R} \\\ & \Rightarrow \varepsilon =6\dfrac{3m\times 10\Omega {{m}^{-1}}}{30+20} \\\ & \therefore \varepsilon =3.6V \\\ \end{aligned}$$ The potential drop per unit length can be obtained as – $$\begin{aligned} & \varepsilon =\phi {{l}_{1}} \\\ & \Rightarrow \phi =\dfrac{\varepsilon }{{{l}_{1}}} \\\ & \Rightarrow \phi =\dfrac{3.6}{3} \\\ & \therefore \phi =1.2m \\\ \end{aligned}$$ Now, let us consider the potential through the cell – $$\begin{aligned} & {{V}_{cell}}={{V}_{0}}\dfrac{R}{R+r} \\\ & \Rightarrow {{V}_{cell}}=2\dfrac{1.5}{1.5+0.5} \\\ & \therefore {{V}_{cell}}=1.5V \\\ \end{aligned}$$ Now, we will get the balancing point of the potentiometer by using the potential drop and the potential drop per unit length as – $$\begin{aligned} & {{V}_{cell}}=\phi {{l}_{2}} \\\ & \Rightarrow {{l}_{2}}=\dfrac{{{V}_{cell}}}{\phi } \\\ & \Rightarrow {{l}_{2}}=\dfrac{1.5}{1.2} \\\ & \therefore {{l}_{2}}=1.25m \\\ \end{aligned}$$ So, the balancing point is 1.25 m from the point A. **The correct answer is option B.** **Note:** The potentiometer is an electrical device which works on Kirchhoff's voltage rule. The device is used to calculate the electromotive forces of the primary cells and are more effective than the voltmeter as the potentiometer works independently in the circuit.