Solveeit Logo
Login

Question

Question: In the figure, a particle has mass m=\(5\)g and a charge q=\(2\times {{10}^{-9}}\) C starts from res...

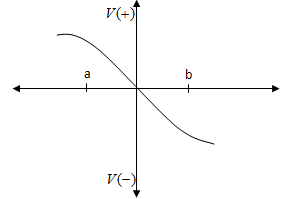
In the figure, a particle has mass m=55g and a charge q=2×10−92\times {{10}^{-9}} C starts from rest at a point a and moves in a straight line to point b. What is its speed at point b?

a)2.65cms−1 b)3.65cms−1 c)4.65cms−1 d)5.65cms−1 \begin{aligned} & a)2.65cm{{s}^{-1}} \\\ & b)3.65cm{{s}^{-1}} \\\ & c)4.65cm{{s}^{-1}} \\\ & d)5.65cm{{s}^{-1}} \\\ \end{aligned}

Explanation

Solution

The charge q is moving on a path of decreasing potential and hence it gets accelerated. The work done, when the charge moves from a to b is negative i.e. we do not have to do any work in moving the charge from a to b. This energy is seen in the form of kinetic energy of the charge in motion.

Complete answer:
Let us call charge q1=3×10−9C{{q}_{1}}=3\times {{10}^{-9}}C and q2=−3×10−9C{{q}_{2}}=-3\times {{10}^{-9}}C for simplicity.
Here are some of the terminologies and formulas we should understand before we begin with the question.
Potential at a point due to a charge: It is an ease in ability of moving a point charge towards a region of influence of a charge(depending on the nature of charges). Potential at a point due to a charge is given by V=Q4π∈∘rV=\dfrac{Q}{4\pi {{\in }_{\circ }}r} and the unit is volt(V).
where QQ is the charge whose potential exists in a region.
rris the distance from the charge QQ,
∈∘{{\in }_{\circ }} is the permittivity of free space.
Potential difference: It is defined as the amount of work done in moving a unit charge towards its region of influence.
Potential due to system of charges: If there are N charges in a system, the potential at a point is given as the sum of potentials due to individual charges by superposition principle i.e.V1+V2+V3+........VN{{V}_{1}}+{{V}_{2}}+{{V}_{3}}+........{{V}_{N}}
Kinetic energy: It is energy gained in motion by an object or particle having mass.
Relation between work done in moving a charge across a given potential difference is given by,
VB−VA=Wq{{V}_{B}}-{{V}_{A}}=\dfrac{W}{q} ….(11)
(Let us call this as equation 1)
The physical quantities in equation 1are explained below
VA{{V}_{A}} is the potential at point a due to charges on either side
VB{{V}_{B}} is the potential at point b due to charges on either side
WWis the work done in moving charge from a to b
q is a point charge moved from a to b

Using superposition principle,
VA={{V}_{A}}= potential at point a due to charge q1{{q}_{1}} ++ potential due to charge q2{{q}_{2}}
VA{{V}_{A}}=3×10−94π∈∘1×10−2+−3×10−94π∈∘2×10−2V\dfrac{3\times {{10}^{-9}}}{4\pi {{\in }_{\circ }}1\times {{10}^{-2}}}+\dfrac{-3\times {{10}^{-9}}}{4\pi {{\in }_{\circ }}2\times {{10}^{-2}}}V
VB={{V}_{B}}= potential at point a due to charge q1{{q}_{1}} ++ potential due to charge q2{{q}_{2}}
VB{{V}_{B}}=3×10−94π∈∘2×10−2+−3×10−94π∈∘1×10−2V\dfrac{3\times {{10}^{-9}}}{4\pi {{\in }_{\circ }}2\times {{10}^{-2}}}+\dfrac{-3\times {{10}^{-9}}}{4\pi {{\in }_{\circ }}1\times {{10}^{-2}}}V
will use 14π∈∘=9×109\dfrac{1}{4\pi {{\in }_{\circ }}}=9\times {{10}^{9}} as k for simplicity.
VA=k3×10−91×10−2+k−3×10−92×10−2V{{V}_{A}}=\dfrac{k3\times {{10}^{-9}}}{1\times {{10}^{-2}}}+\dfrac{k-3\times {{10}^{-9}}}{2\times {{10}^{-2}}}V
Taking k, q1{{q}_{1}} and q2{{q}_{2}} common we get,
VA=k(3×10−9)[11×10−2−12×10−2]V{{V}_{A}}=k(3\times {{10}^{-9}})\left[ \dfrac{1}{1\times {{10}^{-2}}}-\dfrac{1}{2\times {{10}^{-2}}} \right]V
After cross multiplying inside the brackets and subtracting,
VA=k(3×10−9)[1×10−22×10−4]V{{V}_{A}}=k(3\times {{10}^{-9}})\left[ \dfrac{1\times {{10}^{-2}}}{2\times {{10}^{-4}}} \right]V
Substituting for k and further solving we have,
VA=9×109×3×10−9×10−22×10−4V{{V}_{A}}=\dfrac{9\times {{10}^{9}}\times 3\times {{10}^{-9}}\times {{10}^{-2}}}{2\times {{10}^{-4}}}V
VA=27×1022Volts{{V}_{A}}=\dfrac{27\times {{10}^{2}}}{2}Volts
After similarly solving for VB{{V}_{B}}
VB{{V}_{B}}=3×10−94π∈∘2×10−2+−3×10−94π∈∘1×10−2V\dfrac{3\times {{10}^{-9}}}{4\pi {{\in }_{\circ }}2\times {{10}^{-2}}}+\dfrac{-3\times {{10}^{-9}}}{4\pi {{\in }_{\circ }}1\times {{10}^{-2}}}V
VB=k(3×10−9)[12×10−2−11×10−2]V VB=k(3×10−9)[−1×10−22×10−4]V VB=−9×109×3×10−9×10−22×10−4V VB=−27×1022V \begin{aligned} & {{V}_{B}}=k(3\times {{10}^{-9}})\left[ \dfrac{1}{2\times {{10}^{-2}}}-\dfrac{1}{1\times {{10}^{-2}}} \right]V \\\ & {{V}_{B}}=k(3\times {{10}^{-9}})\left[ \dfrac{-1\times {{10}^{-2}}}{2\times {{10}^{-4}}} \right]V \\\ & {{V}_{B}}=\dfrac{-9\times {{10}^{9}}\times 3\times {{10}^{-9}}\times {{10}^{-2}}}{2\times {{10}^{-4}}}V \\\ & {{V}_{B}}=\dfrac{-27\times {{10}^{2}}}{2}V \\\ \end{aligned}
Again using equation 1 and substituting for VB{{V}_{B}} and VA{{V}_{A}},
VB−VA=Wq{{V}_{B}}-{{V}_{A}}=\dfrac{W}{q}
−27×1022\dfrac{-27\times {{10}^{2}}}{2} −27×1022=W2×10−9-\dfrac{27\times {{10}^{2}}}{2}=\dfrac{W}{2\times {{10}^{-9}}}
−27×102×2×10−9=W-27\times {{10}^{2}}\times 2\times {{10}^{-9}}=W
W=−5⋅4×10−6W=-5\cdot 4\times {{10}^{-6}} Joules
This energy is seen in the form of kinetic energy of q, hence
W=W= Change in kinetic energy of the charge.
5⋅4×10−6=Kfinal−Kinitial5\cdot 4\times {{10}^{-6}}={{K}_{final}}-{{K}_{initial}}
Since the initial of the charge q is zero kinetic energy is also zero.
5⋅4×10−6=KFINAL5\cdot 4\times {{10}^{-6}}={{K}_{FINAL}}
Since kinetic energy is given by mv22\dfrac{m{{v}^{2}}}{2}
mv22=5.4×10−6\dfrac{m{{v}^{2}}}{2}=5.4\times {{10}^{-6}}
After cross multiplication on both the sides and substituting for m,
5g is equal to 5×10−35\times {{10}^{-3}} converting to SI unit
v2=2×5.4×10−65×10−3{{v}^{2}}=\dfrac{2\times 5.4\times {{10}^{-6}}}{5\times {{10}^{-3}}}
v=2×5.4×10−65×10−3m/sv=\sqrt{\dfrac{2\times 5.4\times {{10}^{-6}}}{5\times {{10}^{-3}}}}m/s
v=4.6479×10−2m/sv=4.6479\times {{10}^{-2}}m/s
Since 1 cm is 10−2m{{10}^{-2}}m
v=4.65cms−1v=4.65cm{{s}^{-1}}
Hence the correct answer to the question is option c.
Graph of variation of potential between the two charges

Note:

  1. If we see the above fig the charge q moves from a higher potential to lower potential, hence work done is negative. But work done cannot be negative. It is just that some external work must have been done to take charge to higher potential .It is this work that has been converted to kinetic energy and not that the system does work by itself, as it would violate law of conservation of energy. Therefore we have to ignore the sign when we equate it to the kinetic energy of the particle.
  2. The above question cannot be solved by the kinematics equation as the electrostatic force on the charge q is variable.