Question

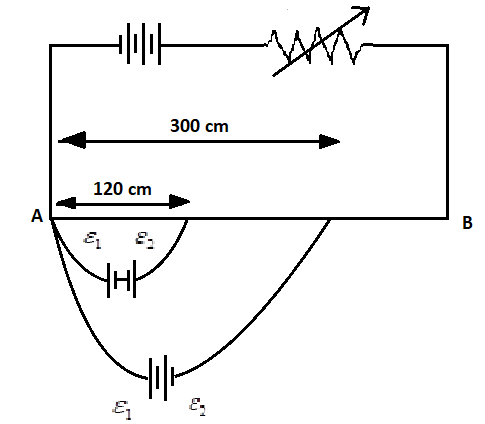
In the figure a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emfs ${\varepsilon _1}$ and ${\varepsilon _2}$ connected in the manner shown are obtained at a distance of $120cm$ and $300cm$ from the end A. Find:
(i) $\dfrac{{{\varepsilon _1}}}{{{\varepsilon _2}}}$ and
(ii) position of null point for the cell ${\varepsilon _1}$.
iii) How is the sensitivity of a potentiometer increased?

Answer 1

Recall all the concepts related to the potential gradient. See the figure carefully and form the equations between the emfs of the cells connected in series. Keep in mind that the connection of cells either opposite or supporting, affects their emfs equation. And also recall all points related to the sensitivity of the potentiometer.

Complete step by step solution:
As we know that, the emf of the cell is directly proportional to the length of the potentiometer given by,
$\varepsilon \propto l$
After removing proportional sign we get a constant k,
$\varepsilon = kl$
Here $k$ be the potential gradient of the potentiometer
For null point $= 120cm$,
As the cells are in the series with each other but connected opposite to each other, we get
${\varepsilon _1} - {\varepsilon _2} = 120k$ ……….(1)
And for null point $= 300cm$,
The cells are in the series with each other and also supporting to each other, we get
${\varepsilon _1} + {\varepsilon _2} = 300k$ …………(2)
On solving equation (1) and (2), we get
${\varepsilon _1} = 210k$ and ${\varepsilon _2} = 90k$
On dividing both we get,
$\dfrac{{{\varepsilon _1}}}{{{\varepsilon _2}}} = \dfrac{{210k}}{{90k}}$
On further solving we get,
$\Rightarrow \dfrac{{{\varepsilon _1}}}{{{\varepsilon _2}}} = \dfrac{7}{3}$

Therefore the answer for the first part is $\dfrac{7}{3}$.

(ii) As we know that,
$\varepsilon = kl$
Here $k$ be the potential gradient of the potentiometer.
From equation (1) and (2),
Null point for the cell ${\varepsilon _2}$ is $90cm$.
And, for the cell ${\varepsilon _1}$, the null point is at $210cm$.

iii) The sensitivity of the potentiometer can be increased by
a) By reducing the current in the circuit by using a rheostat
b) Increasing the length of the potentiometer wire
c) Decreasing the resistance of the circuit

Note: Potentiometer is defined as an instrument which is used for measuring an electromotive force (emf) by balancing emf against the potential difference that is produced by passing a known amount of current. Sensitivity of a potentiometer is defined as the smallest potential difference that is measured by using a potentiometer. By simply decreasing the potential gradient, we can increase the sensitivity.