Question

In the figure, a ladder of mass $m$ is shown leaning against a wall. It is in static equilibrium making an angle$\theta$ with the horizontal floor. The coefficient of friction between the wall and the ladder is ${\mu _1}$ and that between the floor and the ladder is ${\mu _2}$. The normal reaction of the wall on the ladder is${N_1}$ and that of the floor is ${N_2}$. If the ladder is about to slip, then
(A) ${\mu _1} = 0,{\mu _2} \ne 0$ and ${N_2}\tan \theta = \dfrac{{mg}}{2}$
(B) ${\mu _1} \ne 0,{\mu _2} = 0$ and ${N_1}\tan \theta = \dfrac{{mg}}{2}$
(C) ${\mu _1} \ne 0,{\mu _2} \ne 0$ and ${N_2} = \dfrac{{mg}}{{1 + {\mu _1}{\mu _2}}}$
(D) ${\mu _1} = 0,{\mu _2} \ne 0$ and ${N_1}\tan \theta = \dfrac{{mg}}{2}$

Answer 1

Hint : The forces involved are friction, normal forces and weight of the ladder. Also, in this plane, upward forces balances downward forces, leftward forces balances rightward forces, and clockwise torque balances anti-clockwise torque.

Formula used: $f = \mu N$ where $f$ is frictional force and $N$ is the normal force.
$\tau = Fr$ where $\tau$ is the torque and $F$ is any force whose torque about a point is to be found and $r$ is the perpendicular this distance of the force from the point considered.

Complete step by step answer

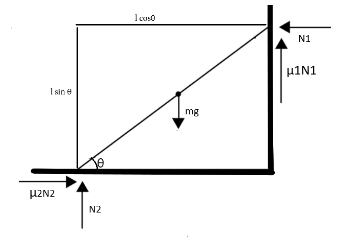
The ladder is said to be in equilibrium. Thus, we must recall the conditions for equilibrium.
First condition of equilibrium, rightward forces balance leftward forces.
Hence, ${\mu _2}{N_2} - {N_1} = 0$
Rearranging the above equation we get,
${\mu _2}{N_2} = {N_1}$
With leftward forces as negative and rightward forces as positive
Second condition of equilibrium, upward forces balance downward forces.
Hence,
${\mu _1}{N_1} + {N_2} - mg = 0$ with upward forces as positive and downward forces as negative.
Replacing ${N_1}$ from the first condition with ${N_1}$ in the second condition, we get
${\mu _1}{\mu _2}{N_2} + {N_2} - mg = 0$
Rearranging the above equation we get,
${N_2}({\mu _1}{\mu _2} + 1) = mg$
Making ${N_2}$ subject of formula, we get
${N_2} = \dfrac{{mg}}{{1 + {\mu _1}{\mu _2}}}$ since $1 + {\mu _1}{\mu _2} = {\mu _1}{\mu _2} + 1$.
This condition thus reveals that for ${\mu _1} \ne 0,{\mu _2} \ne 0$,
${N_2} = \dfrac{{mg}}{{1 + {\mu _1}{\mu _2}}}$ which corresponds to option C.
Hence, option C is a solution.
For the third condition of equilibrium, clockwise torque balances anti-clockwise torque.
Taking the torque about the left end of the ladder, we get
$mg\dfrac{l}{2}\cos \theta - {N_1}l\sin \theta - {\mu _1}{N_1}l\cos = 0$
Dividing the equation by $l\cos$ we get,
$\dfrac{{mg}}{2} - {N_1}\tan \theta - {\mu _1}{N_1} = 0$
Rearranging the above equation we get,
${N_1}\tan \theta = \dfrac{{mg}}{2} - {\mu _1}{N_1}$
Thus, with ${\mu _1} = 0$, ${N_1}\tan \theta = \dfrac{{mg}}{2}$ which corresponds with option D.
Hence, option D is a solution.
The correctness of option D proves the incorrectness of option A, since both cannot be correct except
${N_1} = {N_2}$.
Thus, option A is not a solution.
Finally, to investigate option B from ${N_1}\tan \theta = \dfrac{{mg}}{2} - {\mu _1}{N_1}$ we replace ${N_1}$ with ${\mu _2}{N_2}$ on the right hand side.
Thus, ${N_1}\tan \theta = \dfrac{{mg}}{2} - {\mu _1}{\mu _2}{N_2}$.
Making ${\mu _2} = 0$ we get
${N_1}\tan \theta = \dfrac{{mg}}{2}$
Hence, option B is also a solution.
Hence, the correct options are B, C and D.

Note
Usually, in equilibrium we can take the torque about any point of the ladder, such as the center, or the right end of the ladder. However, using the left end of the ladder quickly reveals an expression comparable to one of the options.