Question

In the figure, a fish watcher watches a fish through a $3.0cm$ thick glass wall of a fish tank. The watcher is in level with the fish, the index of refraction of the glass is $8/5$ and that of the water is $4/3$.

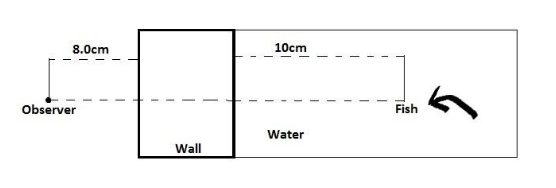
a. To the fish, how far away does the watcher appear to be?
b. To the watcher, how far away does the fish appear to be?

Answer 1

The apparent depth depends on refractive index and the real depth. Since the fish is in water, we consider the real distance of the fish from the wall in the case of calculating the distance of the watcher from the fish. The distance of the fish from the observer can be calculated by finding the real depth.
Formula Used: The formulae used in the solution are given here.
Apparent depth ${h_{apparent}} = \dfrac{H}{\eta }$ where $H$ is the real depth and $\eta$ is the refractive index.

Complete Step by Step Solution: It has been given that a fish watcher watches a fish through a $3.0cm$ thick glass wall of a fish tank. The watcher is in level with the fish, the index of refraction of the glass is $8/5$ and that of the water $4/3$.
Real Depth is the actual distance of an object beneath the surface, as would be measured by submerging a perfect ruler along with it.
Apparent depth in a medium is the depth of an object in a denser medium as seen from the rarer medium. Its value is smaller than the real depth.
Mathematically, apparent depth ${h_{apparent}} = \dfrac{H}{\eta }$ where $H$ is the real depth and $\eta$ is the refractive index.
The apparent distance is needed to be found.
Now refractive index of the wall is given by, ${\eta _{wall}} = \dfrac{{{\eta _{water}}}}{{{\eta _{glass}}}}$ where ${\eta _{water}}$ is the refractive index of water and ${\eta _{glass}}$ is the refractive index of glass.
Assigning the value given in the question, we have, ${\eta _{wall}} = \dfrac{{4/3}}{{8/5}}$.
Now, the distance of the watcher from the fish is given by, ${h_{apparent}} = \dfrac{H}{\eta }$.
We will thus compute the values to get the answer.
$3 \times \dfrac{4}{3} + 3 \times \dfrac{{4/3}}{{8/5}} + 10 = \dfrac{{139}}{6}cm$
$= 23.167cm$.
Here, since the fish is in the water, the real distance shall suffice.
The distance of the fish from the watcher is also found in the same way. Since the observer is in air, we will compute the values in the formula.
We have,
$\dfrac{{10}}{{4/5}} + \dfrac{3}{{8/5}} + 8 = \dfrac{{139}}{8}cm$
$= 17.375cm$
Hence the answers are given.

Note: This phenomenon occurs due to the property of light called refraction of light. When immersing a stick in water, the rays of light pass from rarer medium to denser medium and they move towards the normal. So the part of the stick immersed in water appears to be broken towards the normal drawn at the interface and gives an apparent bending. It also appears short like being raised up in the water.