Question
Question: In the figure, a block of weight \(60\,N\) is placed on a rough surface. The coefficient of friction...
In the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface if 0.5. What should be the weight W such that the block does not slip on the surface.
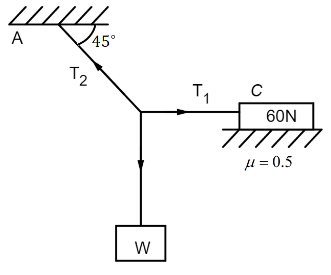
Solution
Any block placed on a rough surface (having some coefficient of friction) moves when the force applied on it is greater than limiting static friction (or limiting friction) whose value is equals to the normal force times the coefficient of friction.
Formula used:
The mathematical expression for static friction is given by,
f=μN
where f is the frictional force and N is the normal force.
Complete step by step answer:
Let’s analyse the blocks first
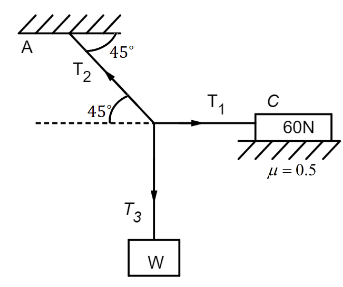
Block C: Forces acting on Block C are:
-Normal reaction force from surface on which it is kept (N)
-Tension force (T1)
-Its weight (60N)
-Static frictional force (f)
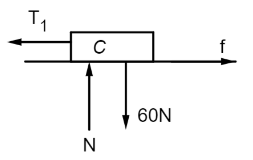
As block C is in equilibrium
∴∑Fx=0
⇒f−T1=0
Hence f=T1 ……………..…………………(i)
also ∑Fy=0
⇒N−60=0 or N=60 …………..(ii)
The frictional force on block C:
f=μN=0.5×60=30N………(iii) [using (ii)]
Using equation (i) and (iii) we get T1=30N………….(iv)
Block B: Forces acting on Block B are:
Tension force (T3)
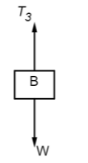
Its weight (W). As block B is in equilibrium
∴∑Fy=0 ⇒T3−W=0
Hence, T3=W ………………………………..(v)
As the junction P is in equilibrium so at point P
∑Fx=0
∴T1=T2×21……………..(vi)
∑Fy=0
∴T3=T2×21…………….(vii)
Now using equation (vi)and(iv)we get
T1=T2×21
⇒T2=2T1
∴T2=302N……………(viii)
Finally, using equation (v),(vii) and (viii)
T3=302×21=30N and T3=W
Hence W=30Newtons.
Note: If a block is at rest and keeps on resting on applying force then applied force is equal to the frictional force on the block as net force on the block = 0 in the condition of equilibrium. A body remains at rest if no external force is applied to it.
