Question

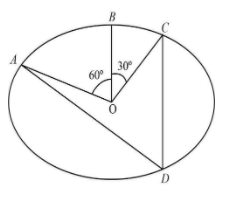
In the figure A, B and C are three points on a circle with centre O such that $\angle BOC = 30^\circ$ and$\angle AOB = 60^\circ$. If D is a point on the circle other than the arc ABC, find$\angle ADC$.

Answer 1

To solve this kind of problem use the theorem which states that the angle created by an arc at the centre is twice of the angle created by the same arc at any point on the remaining part of the circle.

Complete step-by-step solution
Given, in a circle angle made by arc ABC on its centre are $\angle BOC = 30^\circ$and$\angle AOB = 60^\circ$.
In a circle angle made by arc ABC on the centre of circle is,
$\angle AOC = \angle BOC + \angle AOB$
Substitute the values of angle in above equation,
$\begin{array}{c} \angle AOC = 30^\circ + 60^\circ \\\ = 90^\circ \end{array}$
We have to determine the angle$\angle ADC$, which is the angle made by the same arc ABC on the periphery of the circle. So it will be the half of the angle made by arc ABC on its centre.
$\angle ADC = \dfrac{1}{2}\angle AOC$
Substitute the value of $\angle AOC$in above equation,we get
$\begin{array}{c} \angle ADC = \dfrac{1}{2} \times 90^\circ \\\ = 45^\circ \end{array}$

Note: Here we have to remember that both angles should be taken in the same direction, if the centre angle is anticlockwise then the periphery angle should also be measured in anticlockwise direction.