Question

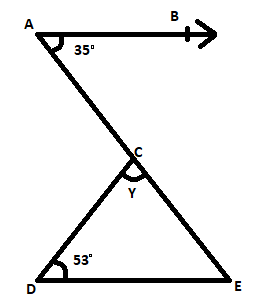
In the fig if AB | | DE, $\angle BAC\,\,=\,\,35{}^\text{o}\,\,and\,\,\angle CDE\,\,=\,\,53{}^\text{o},$ find $\angle DCE$?

Answer 1

Use the alternate angle method to solve the given problem
Alternate angle: When two lines are crossed by other lines the pair of angle on the opposite side of the transversal is called alternate angle

Complete step by step solution:
Given that
AB | | DE
$\angle BAC\,\,=\,\,35{}^\text{o}$and$\angle CDE\,\,=\,\,53{}^\text{o}$
Let $\angle DCE\,\,=\,\,y$
In order to solve the given problem we need to use the following alternate angle method.
$\angle BAC\,=\,\angle DEC\,\,=\,\,35{}^\text{o}$ (Alternate interior angle)
$\angle CDE\,\,=\,\,53{}^\text{o}$given
We know that sum of the interior angle of the triangle is $180{}^\text{o}$
In $\Delta DCE$
$\angle CDE+\angle DEC+\angle DCE=180\,\,\,\,\,\,\,\,........(1)$
Substitute the value of $\angle CDE+\angle DEC$ in the equation $(1)$
$53{}^\text{o}+35{}^\text{o}+y=180{}^\text{o}$
$y=180{}^\text{o}88{}^\text{o}$
$y=92{}^\text{o}$

Note: Students should be careful about using the concept of the sum of the interior angle of the triangle.
The problem is also solved by the property of angles made between two parallel lines.