Solveeit Logo
Login

Question

Question: In the dissociation of \(PC{l_5}\) as \(PC{l_5}(g) \rightleftarrows PC{l_3}(g) + C{l_2}(g)\) If th...

In the dissociation of PCl5PC{l_5} as PCl5(g)⇄PCl3(g)+Cl2(g)PC{l_5}(g) \rightleftarrows PC{l_3}(g) + C{l_2}(g)
If the degree of dissociation is α\alpha at equilibrium pressure P, then what is the equilibrium constant for this reaction?
A) Kp=α21+α2P{K_p} = \dfrac{{{\alpha ^2}}}{{1 + {\alpha ^2}P}}
B) Kp=α2P21−α2{K_p} = \dfrac{{{\alpha ^2}{P^2}}}{{1 - {\alpha ^2}}}
C) Kp=P21−α2{K_p} = \dfrac{{{P^2}}}{{1 - {\alpha ^2}}}
D) Kp=α2P1−α2{K_p} = \dfrac{{{\alpha ^2}P}}{{1 - {\alpha ^2}}}

Explanation

Solution

Calculate the amount of products and reactants initially and at equilibrium. Calculate the partial pressure of both the reactants and products which is the product of mole fraction and the total pressure. Substitute these partial pressure values in the equilibrium constant formula to calculate its value.

Complete step-by-step solution: Initially, let us calculate the amount of products and reactants at t=0t = 0 and at equilibrium with the given degree of dissociation asα\alpha . The following table shows the amount of each substance.

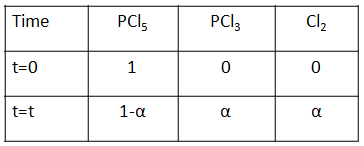
From this table, we can calculate the total number of moles as 1−α+α+α=1+α1 - \alpha + \alpha + \alpha = 1 + \alpha
We know that mole fraction is the number of moles of a substance divided by the total number of moles. From this we calculate the partial fraction of each substance.
PPCl5=1−α1+αP{P_{PC{l_5}}} = \dfrac{{1 - \alpha }}{{1 + \alpha }}P , PPCl3=α1+αP{P_{PC{l_3}}} = \dfrac{\alpha }{{1 + \alpha }}P and PCl2=α1+αP{P_{C{l_2}}} = \dfrac{\alpha }{{1 + \alpha }}P
For the given reaction, the formula for equilibrium constant is Kp=PPCl3.PCl2PPCl5{K_p} = \dfrac{{{P_{PC{l_3}}}.{P_{C{l_2}}}}}{{{P_{PC{l_5}}}}}
By substituting the values of partial pressure of each substance, we get Kp=αP1+α.αP1+α1−α1+αP{K_p} = \dfrac{{\dfrac{{\alpha P}}{{1 + \alpha }}.\dfrac{{\alpha P}}{{1 + \alpha }}}}{{\dfrac{{1 - \alpha }}{{1 + \alpha }}P}}
By solving this, we get Kp=α2P1−α2{K_p} = \dfrac{{{\alpha ^2}P}}{{1 - {\alpha ^2}}}

Therefore, the value of equilibrium constant for the given reaction with the degree of dissociation α\alpha is Kp=α2P1−α2{K_p} = \dfrac{{{\alpha ^2}P}}{{1 - {\alpha ^2}}} i.e. option D.

Note: Before deriving the formula for equilibrium constant for any reaction, it is always important to balance the equation since the number of moles becomes the exponential value of the concentration or pressure. Since in this reaction, all the compounds are only one molecule, the exponential value of the partial pressures was one.