Question

In the diagram, the potential difference between A and B is $60{\rm{ V}}$. The potential difference across $6{\rm{ }}\mu {\rm{F}}$ capacitor is ________V.

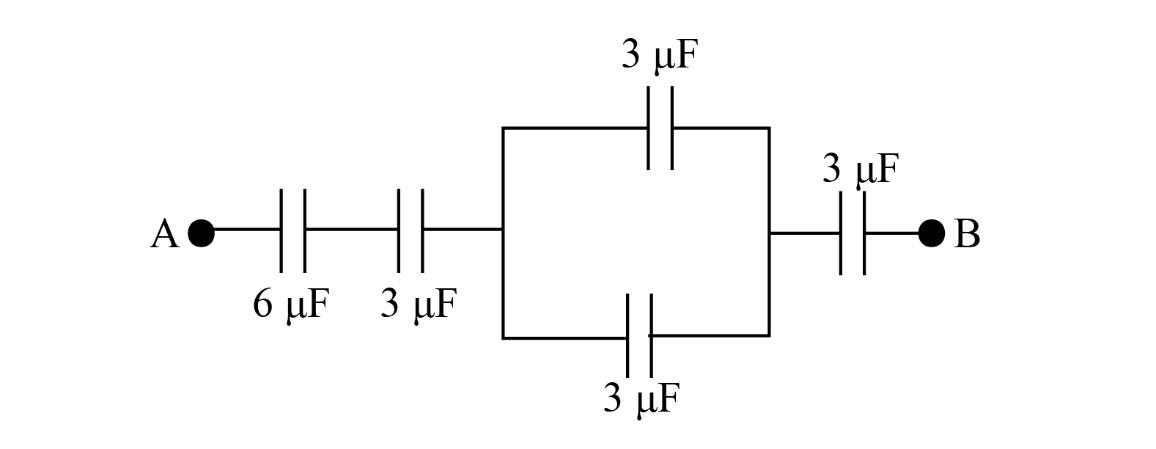
A 10
B 5
C 20
D 4

Answer 1

We will reduce the given network by using the concept of equivalent capacitance when two capacitors are in parallel and series combination. We also know that when two capacitors are in series combination, the charge across them is the same.

Complete step by step answer:
It is given that the potential difference between A and B is $V = 60{\rm{ V}}$.
We have to find the value of potential difference $V'$ across $6{\rm{ }}\mu {\rm{F}}$ capacitor.

Let us write the expression for equivalent capacitance when two capacitors ${C_1}$ and ${C_2}$ are in parallel combination.
$C = {C_1} + {C_2}$

On observing the given network closely, we can say that two capacitors of equal capacitance $3{\rm{ }}\mu {\rm{F}}$ are in parallel combination.

Substitute $3{\rm{ }}\mu {\rm{F}}$ for ${C_1}$ as well as ${C_2}$ in the above expression.

C = 3{\rm{ }}\mu {\rm{F}} + 3{\rm{ }}\mu {\rm{F}}\\\ {\rm{ = 6 }}\mu {\rm{F}} \end{array}$$ So we can replace the parallel combination of capacitors having an equal capacitance of $$3{\rm{ }}\mu {\rm{F}}$$ by a capacitor of equivalent capacitance of $$6{\rm{ }}\mu {\rm{F}}$$and the given network can be reduced as shown below: 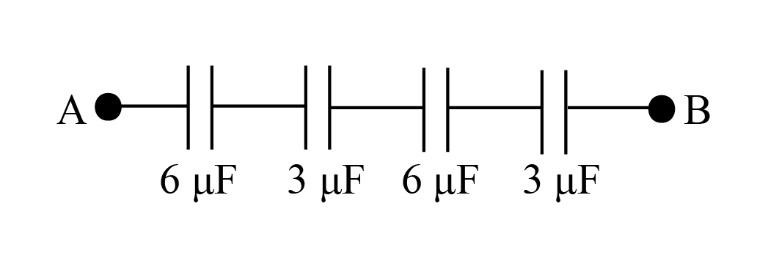 Write the expression for the equivalent capacitance of three capacitors having capacitance $${C_3}$$, $${C_4}$$ and $${C_5}$$ when they are connected in series. $$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}} + \dfrac{1}{{{C_5}}}$$ From the reduced network, we can say that the three capacitors on the right hand side are in series combination. Substitute $$3{\rm{ }}\mu {\rm{F}}$$ for $${C_3}$$, $${\rm{6 }}\mu {\rm{F}}$$ for $${C_4}$$ and $$3{\rm{ }}\mu {\rm{F}}$$ for $${C_5}$$ in the above expression. $$\begin{array}{l} \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{3{\rm{ }}\mu {\rm{F}}}} + \dfrac{1}{{{\rm{6 }}\mu {\rm{F}}}} + \dfrac{1}{{3{\rm{ }}\mu {\rm{F}}}}\\\ \dfrac{1}{{{C_{eq}}}} = \dfrac{5}{{{\rm{6 }}}}\mu {\rm{F}}\\\ {C_{eq}} = \dfrac{6}{{{\rm{5 }}}}\mu {\rm{F}} \end{array}$$ Now the network is reduced into a form in which two capacitors of $$\dfrac{6}{{{\rm{5 }}}}\mu {\rm{F}}$$ capacitance and $$6\mu {\rm{F}}$$ capacitance are in series. The value of charge for $$6\mu {\rm{F}}$$ capacitor is equal to the product of the voltage and its capacitance. $${Q_1} = V'6\mu {\rm{F}}$$ Here V’ is the voltage across $$6\mu {\rm{F}}$$ capacitor. The value of charge for $$\dfrac{6}{5}\mu {\rm{F}}$$ capacitor is equal to the product of the voltage and its capacitance. $${Q_2} = V\dfrac{6}{5}\mu {\rm{F}}$$ Here V is the voltage across $$\dfrac{6}{5}\mu {\rm{F}}$$ capacitor. We know that the charge in series combinations of two capacitors is the same. So we write: $${Q_1} = {Q_2}$$ Substitute $$V'6\mu {\rm{F}}$$ for $${Q_1}$$ and $$V\dfrac{6}{5}\mu {\rm{F}}$$ for $${Q_2}$$ in the above expression. $$V'6\mu {\rm{F}} = V\dfrac{6}{5}\mu {\rm{F}}$$……(1) It is given that the potential difference between point A and B is $$60{\rm{ V}}$$so that we can write: $$\begin{array}{l} V + V' = 60{\rm{ V}}\\\ V = 60{\rm{ V}} - V' \end{array}$$ Substitute $$60{\rm{ V}} - V'$$ for V in equation (1). $$\begin{array}{l} V'6\mu {\rm{F}} = \left( {60{\rm{ V}} - V'} \right)\dfrac{6}{5}\mu {\rm{F}}\\\ V' = 10{\rm{ V}} \end{array}$$ Therefore, the value of the potential difference across $$6{\rm{ }}\mu {\rm{F}}$$ capacitor is $$10{\rm{ V}}$$ **So, the correct answer is “Option A”.** **Note:** It would be an added advantage to remember the equivalent capacitance of two capacitors when they are in parallel or series combination. Take care while substituting the value of V in equation (1).