Question

In the diagram shown coefficient of friction between 2kg block and 4kg block is $\mu =0.1$ and between $4kg$ and ground is $\mu =0.2$ then answer the following questions. ( $t$ is time)

1. Force of friction on $2kg$ at $t=\dfrac{1}{2}s$ will be:

& \text{A)1N towards left} \\\ & \text{B)1N towards right} \\\ & \text{C) 0N} \\\ & \text{D) 2N towards left} \\\ \end{aligned}$$ 2) At $$t=4s$$ the friction between $$4kg$$ bock and ground will be: $$\begin{aligned} & \text{A)2N towards right} \\\ & \text{B)4N towards left} \\\ & \text{C) 0N} \\\ & \text{D) 2N towards left} \\\ \end{aligned}$$ 3) The graph of friction force acting on $$4kg$$ and ground as a function of time. 

Answer 1

Here first draw the free body diagram of the block and determine what all forces are acting on them. Here the masses of the two blocks and coefficient of friction between two blocks and between ground and block 2 are given. The external force is given as a function of time. Hence, we can find the external force acting on the block at different times, thereby the frictional forces acting on each block at various times.

Formula used:
${{N}_{1}}={{m}_{1}}g$
${{F}_{\max }}={{\mu }_{1}}{{N}_{1}}$

Complete step by step solution:

Given,
Mass of the block 1, ${{m}_{1}}=2kg$
Mass of the block 2, ${{m}_{2}}=4kg$
Coefficient of friction between two blocks, ${{\mu }_{1}}=0.1$
Coefficient of friction between block 2 and ground, ${{\mu }_{2}}=0.2$
External force, $F=2t$
Where, $t$ is the time in seconds.
1)

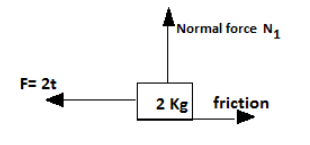
At $t=\dfrac{1}{2}s$ external force will be,
$F=2\times \dfrac{1}{2}=1N$ ---------- (1)
Maximum frictional force between 2 blocks is,
${{F}_{\max }}={{\mu }_{1}}{{N}_{1}}$
Where ${{N}_{1}}$is the normal force acting block 1.
We have,
${{N}_{1}}={{m}_{1}}g$
Where,
${{m}_{1}}$ is the mass of the block 1.
$g$is the acceleration due to gravity ($g=10m/{{s}^{2}}$)
For block 1, $N=2\times 10=20$ and $\mu =0.1$
Substitute the above value in equation 1, we get,
${{F}_{\max }}=0.1\times 20=2N$ -------- (2)
Comparing equations 1 and 2 we can see that the applied force is less than the frictional force.
Hence, the friction on $2kg$ at $t=\dfrac{1}{2}s$ is, ${{F}_{net}}=2-1=1N$ towards right.
Therefore, the answer is option B.
2) At $t=4s$ the external force acting is,
$F=2\times 4=8N$
The frictional force acting between two blocks is $2N$. Then, the tension acting on the block 2 will be,
$T=8-2=6N$
But, a frictional force is also acting between $4kg$ block and ground.

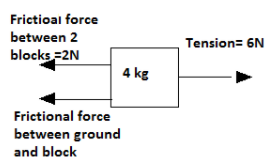
At equilibrium, these forces will balance.
$2+F=6N$
Then,
$F=6-2=4N$
Thus, at$t=4s$ the friction between $4kg$ bock and ground will be $4N$
3) at t=0,1
For block 1,
External force, $F=2t$ and frictional force will be same as the external force, $f=2t$
For block 2,
Force acting on the right hand side is $F=2t$, frictional force between ground and block will be same as the external force, $f=2t$
For $t>1s$,
For block 1,
Frictional force will be maximum, $f=2N$ and tension is also acting on the block 1.
Tension, $T=2t-2$
For block 2,
Tension on block 2 is, $T=2t-2$, frictional force between ground and block is, $f=2N$
At $t<2$,
Tension $2t-2$is less than frictional force $2N$
Thus, at $t=\left( 1,2 \right)$
Frictional force, $f=2-2t+2=4-2t$ towards right.
For $t>2s$
External force is increased hence, the tension increases and the frictional force will act towards the left.
From the above values we can see that, the correct graph is option a.

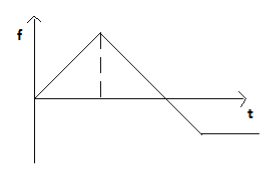
Therefore, the answer is option A.

Note:
Friction is of two types: static friction and kinetic friction. Static friction is applied on the body at rest, or the body which is about to move. Static friction opposes the movement of the body. Its value is equal to applied force till the body remains in static position. i.e., it self-adjusts its value according to applied force.