Question
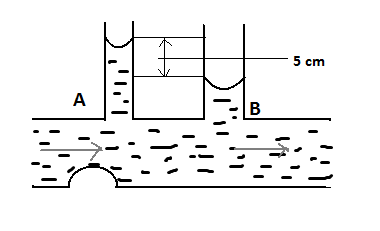
Question: In the diagram shown below, the difference between the tubes of the manometer is 5 cm, the cross-sec...
In the diagram shown below, the difference between the tubes of the manometer is 5 cm, the cross-sections at A and B are 6 sq mm and 10 sq mm respectively. The rate at which water flows through the tube is;(g=10ms−2)
(A) 7.5 cc/sec
(B) 8.0 cc/sec.
(C) 10.0 cc/sec.
(D) 12.5 cc/sec.
Solution
This problem uses Bernoulli's theorem. Bernoulli's theorem is the pressure version of energy conservation. It is also similar to conservation of momentum.
Complete solution:
Bernoulli’s principle: In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy. Bernoulli's principle can be applied to various types of fluid flow, resulting in various forms of Bernoulli's equation; there are different forms of Bernoulli's equation for different types of flow.
The simplest one being;
P+21ρv2=C.
Here, P is the pressure at the surface of the liquid due to air, ρ is the density of the fluid and v is the velocity of the fluid and C is constant.
Bernoulli's theorem also describes the relationship between a fluid's velocity and cross-sectional area. Mathematically it is written as A1v1=A2v2.
Now in this case, the difference between the tubes is given viz. 5cm= 0.05 meters.
So first we find the velocity relation in the two tubes.
Hence by applying Bernoulli’s theorem we get;
A1v1=A2v2 here, A1=6mm2 and A2=10mm2 ;
Thus, 6v1=10v2
Thus v1=35v2 (equation:1)
Now apply Bernoulli’s theorem of conservation of pressure;
P1+21ρv12=P2+21ρv22
Solving the equation further we get;
P1−P2=21ρ(v22−v12)
P1−P2=21ρ(v22−925v22) (from equation: 1)
Now we know that, P2−P1=ρg(h2−h1)=0.05ρg (given)
0.05ρg=21ρ(916v22)
Solving the above equation we get,
v2=0.75ms−2
Therefore, rate of flow is mathematically Area X velocity;
Rate=A2v2=75×10−1cm3sec−1
Hence option A is correct.
Note: (1) The units must be converted very carefully
(2) Av is the rate of flow of fluid so Bernoulli’s principle states that rate of flow is constant.
