Question
Question: In the diagram \[\overrightarrow {OA} = a\] and \[\overrightarrow {OB} = b\]. a. Find in terms of ...
In the diagram OA=a and OB=b.
a. Find in terms of a and b:
i. OC
ii. OE
iii. OD
iv. DC
v. DE
b. If∣a∣=1 and ∣b∣=2,
find:
i. OC
ii. OE
iii. OD
Solution
This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. To solve this question we need to know how to compare one vector value with another vector value. We need to know how to find the magnitude of the particular vector. Also, we need to know the formula for finding a magnitude of a vector. Also, we need to know the Pythagoras theorem to solve this question.
Complete step by step solution:
In the given question we have
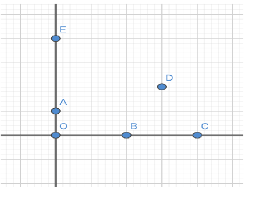
(Here OA=a and OB=b)
Let’s solve the case: a
i. OC
We know thatOB=b.
From the figure we getBC=OB
So, we get
\overrightarrow {OE} = 4 \times \overrightarrow {OA} \\
\overrightarrow {OE} = 4 \times a \\
\overrightarrow {OE} = 4a \\
(Herethevalueof\overrightarrow {OE} isfourtimesof\overrightarrow {OA} )iii.\overrightarrow {OD} $$
Let’ see the given figure below,
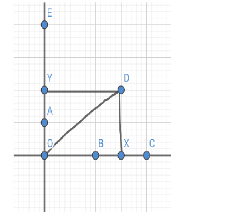
(Here we mark the points X and Y in the above figure to make easy calculation)
From the above figure we get,
OD2=OX2+XD2 (By using Pythagoras theorem in a triangle ODX)
Here, OX=OB+2BC (Here 2BC can also be expressed as BX)
We know that,
So, we can write
OX2=(b+2b)2
(Let’s convert the mixed fraction term into simple fraction term)
XD = OY \\
OY = OA + AY = a + a = 2a \\
O{Y^2} = X{D^2} = 4{a^2} \\
(HereOYisequaltotwotimesofOA)So,wegetO{D^2} = O{X^2} + X{D^2}(ByusingPythagorastheoreminthetriangleODX)O{D^2} = \dfrac{{9{b^2}}}{4} + 4{a^2}\overrightarrow {OD} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} iv.\overrightarrow {DC} $$
To solve the above-mentioned term the following figure will help us,
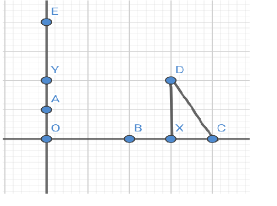
So, we get
DC2=XD2+XC2
We know that,
XD2=4a2 (This equation is already solved in the above steps)
XC2=(2b)2=4b2 (Here we use the
formula(ba)m=bmam)
We get, DC2=XD2+XC2
\overrightarrow {OC} = 2b \\
\left| {\overrightarrow {OC} } \right| = 2\left| b \right| = 2 \times 2 = 4 \\
(Herewesubstitute\left| b \right| = 2)ii.\left| {\overrightarrow {OE} } \right|$$
We know that,
\overrightarrow {OC} = 2b \\
\overrightarrow {OE} = 4a \\
\overrightarrow {OD} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} \\
\overrightarrow {DC} = \sqrt {4{a^2} + \dfrac{{{b^2}}}{4}} \\
\overrightarrow {DE} = \sqrt {\dfrac{{9{b^2}}}{4} + 4{a^2}} \\
\left| {\overrightarrow {OC} } \right| = 4 \\
\left| {\overrightarrow {OE} } \right| = 4 \\
\left| {\overrightarrow {OD} } \right| = \sqrt {13} \\
\\
\\
